Pyomo : Optimisation sous contraintes en Python

✍Luc Gibaud / Temps de lecture : 10 minutes.
Pyomo est une bibliothèque d’optimisation sous contraintes open-source, disponible sur Python, à l’initiative du centre de recherche en informatique des Sandia National Laboratories et fait partie du projet COIN-OR. L’objectif de cet article est de vous présenter comment utiliser Pyomo au travers d’un exemple pouvant être facilement adapté à l’activité de nombreuses entreprises.
Problématique
Prenons l’exemple d’une entreprise spécialisée dans la vente de T-shirts qui, pour l’année à venir, souhaite établir un planning prévisionnel des T-shirts à produire et à vendre chaque mois, afin d’optimiser ses bénéfices. La société a préalablement fait une estimation de la demande mensuelle de T-shirts de ses clients au cours de l’année.
On sait qu’un T-shirt se vend 10€, coûte 4€ à produire et coûte chaque mois 1,1€ à stocker. La société dispose également d’un stock de 200 T-shirts au début de l’année.
Par ailleurs, voici les données dont nous disposons, stockées dans un DataFrame Pandas df :
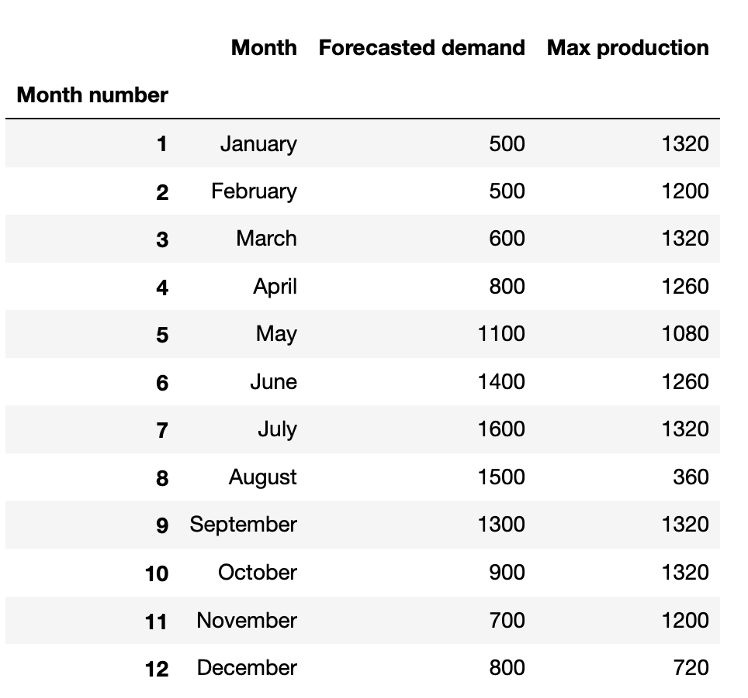
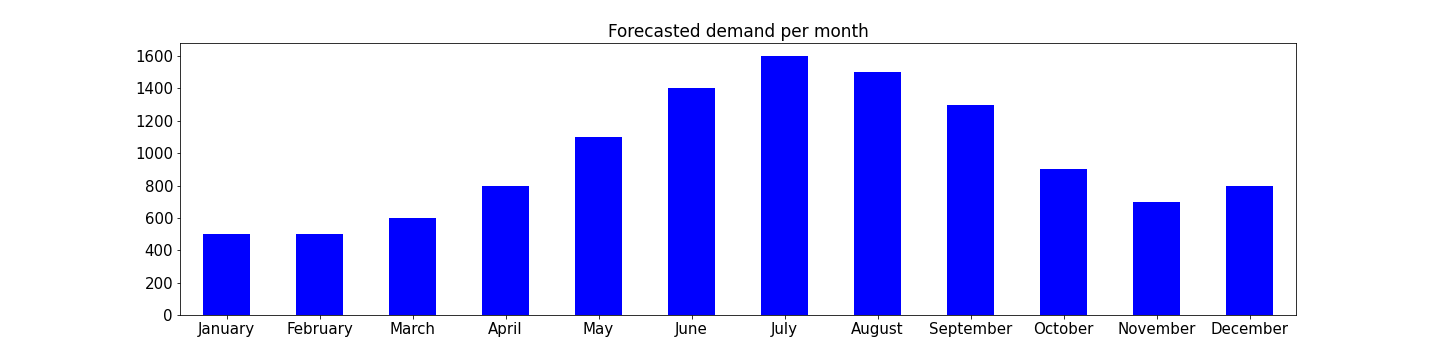
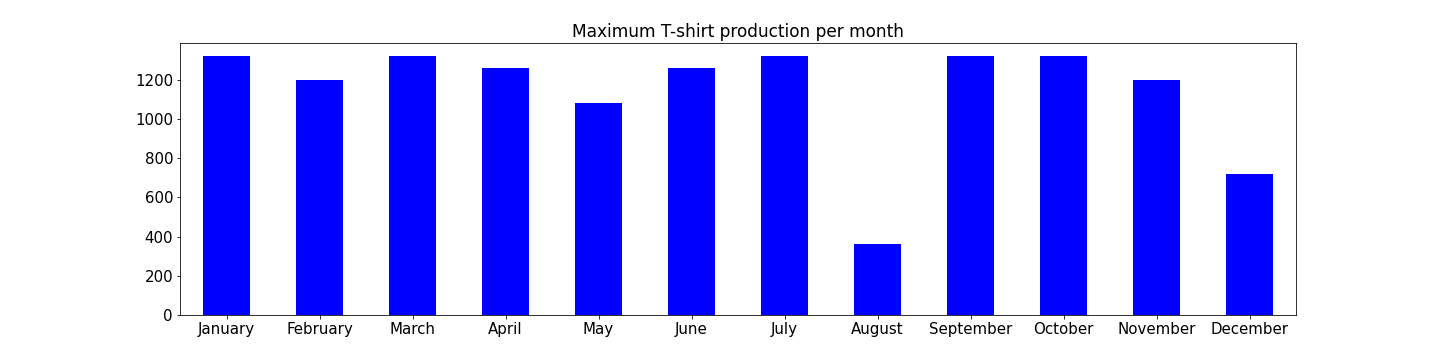
On remarque que la demande est beaucoup plus forte en été que les autres mois de l’année. De plus, la quantité de T-shirts qui peuvent être produits chaque mois varie peu, sauf en août et décembre, où cette quantité maximale est moindre, en raison des congés annuels.
Création du modèle
Pour commencer, nous créons le modèle en Pyomo:
import pyomo.environ as pyo model = pyo.ConcreteModel(doc="Optimization model")
Définition d’un index
Nous créons un index, qui servira par la suite à créer, et parcourir les variables que nous définirons. Comme notre objectif final est d’obtenir un planning prévisionnel de la quantité de T-shirts à produire et à vendre chaque mois, nous créons un index parcourant les mois (les entiers de 1 à 12) :
model.months = pyo.Set(initialize=(i for i in df.index), doc="Index of variables")
Définition des variables
Pour commencer, définissons des variables de productions, une variable de production par mois, qui correspond à la quantité de T-shirts produits ce mois :
def func_bounds_productions(model, month): return (0, df["Max production"].to_dict()[month]) model.productions = pyo.Var(model.months, domain=pyo.NonNegativeIntegers, bounds=func_bounds_productions, doc="Optimized productions")
Concrètement, une variable est définie pour chaque valeur prise par l’index défini précédemment. On pourra donc par la suite faire appel à la variable de production du mois de mars grâce à la syntaxe model.productions[3] par exemple.
Chaque mois, on ne peut produire qu’un nombre entier positif de T-shirts, c’est ainsi que nous avons défini comme domaine des variables de production pyomo.environ.NonNegativeIntegers.
De plus, nous souhaitons que les variables de production d’un mois donné ne puissent dépasser la capacité maximale de production de T-shirts de ce mois. Pour ce faire, nous utilisons le paramètre bounds de pyomo.environ.Var.
De la même manière, nous définissons également les variables de ventes. Ici, nous souhaitons que les variables de ventes d’un mois donné ne puissent dépasser la demande prévisionnelle en T-shirts de ce mois :
def func_bounds_sales(model, month): return (0, df["Forecasted demand"].to_dict()[month]) model.sales = pyo.Var(model.months, domain=pyo.NonNegativeIntegers, bounds=func_bounds_sales, doc="Optimized sales")
Des variables de stocks sont également définies, la syntaxe est allégée car nous ne souhaitons pas que ces variables soient bornées :
model.stocks = pyo.Var(model.months, domain=pyo.NonNegativeIntegers, doc="Optimized stocks")
Définition des paramètres
Les valeurs des paramètres sont fixes et ne varient pas au cours de l’optimisation. Nous définissons ainsi, le prix de vente unitaire, le coût de production unitaire, le coût de stockage mensuel unitaire et le volume des stocks initiaux :
model.sale_price = pyo.Param(default=10, doc="Unit selling price") model.prod_cost = pyo.Param(default=4, doc="Unit production cost") model.stock_cost = pyo.Param(default=1.1, doc="Monthly unit storage cost") model.initial_stocks = pyo.Param(default=200, doc="Initial stocks")
De la même manière que pour définir les variables, nous pouvons utiliser l’index pour définir une série de paramètres, mais ce n’est pas nécessaire dans cet exemple.
Définition de la fonction objectif
Le but d’un problème d’optimisation est de minimiser ou de maximiser la fonction objectif afin d’atteindre un optimum. Ici, on souhaite maximiser les bénéfices annuels de l’entreprise, c’est-à-dire le montant total rapporté par les ventes de T-shirts, duquel on déduit les coûts de production ainsi que les coûts de stockage. Grâce à Pyomo, on peut définir cette fonction comme suit :
def func_objective(model): objective_expr = sum([ (model.sales[v] * model.sale_price) - (model.productions[v] * model.prod_cost) - (model.stocks[v] * model.stock_cost) for v in model.months ]) return objective_expr model.objective = pyo.Objective(rule=func_objective, sense=pyo.maximize, doc="Objective function: maximize margin")
Définition des contraintes
1ère série de contraintes : Équilibre entre ventes, production et stocks
L’objectif de cette première liste de contraintes est de vérifier que, chaque mois, la somme des ventes ne peut pas excéder la somme de la production de ce mois et du stock restant à la fin du mois précédent. En Pyomo, on peut écrire cette contrainte comme suit :
model.constraint_sales_prod_stocks = pyo.ConstraintList(doc="Balance sales, productions and stocks") for month in model.months: if month==1: # January constraint model.constraint_sales_prod_stocks.add( model.sales[1] <= model.initial_stocks + model.productions[1] ) else: # Constraints from February to December model.constraint_sales_prod_stocks.add( model.sales[month] <= model.stocks[month - 1] + model.productions[month] )
On utilise une liste de contraintes, qui permet de regrouper des contraintes similaires. Les lignes de code précédentes définissent en réalité bien 12 contraintes distinctes.
2nd série de contraintes : Contraintes des stocks
Par ailleurs, chaque mois, la variable de stock doit être égale aux stocks du mois précédent, auxquels on ajoute la production, et on soustrait la vente du mois courant, on définit ainsi la liste de contrainte suivante :
model.constraint_stocks = pyo.ConstraintList(doc="Stocks constraints") for month in model.months: if month==1: # January constraint model.constraint_stocks.add( model.stocks[1] == model.productions[1] - model.sales[1] + model.initial_stocks ) else: # Constraints from February to December model.constraint_stocks.add( model.stocks[month] == model.productions[month] - model.sales[month] + model.stocks[month-1] )
Résolution du problème d’optimisation
Une fois le problème ainsi défini, l’optimisation se fait grâce à un solveur, c’est-à-dire un algorithme d’optimisation. Il existe plusieurs, dans notre cas, nous allons utiliser CBC (COIN-OR Branch and Cut), un solveur permettant la résolution de problème linéaires, écrit en C++.
from pyomo.opt import SolverFactory
solver = SolverFactory("cbc", executable="../solvers/cbc-osx/cbc")
results = solver.solve(model)
Le chemin indiqué dans le paramètre executable est le chemin de l’exécutable CBC. Pour le lecteur qui souhaite essayer rapidement un solveur, je conseille de consulter le site d’AMPL (Open Source Solvers), qui répertorie les liens permettant de télécharger les exécutables de plusieurs solveurs open-source (dont CBC). Cela évite l’étape, parfois fastidieuse, de compiler le code source des solveurs.
À la fin de l’optimisation, chaque variable définie se voit attribuer une valeur. Par exemple, pour accéder au volume de vente du mois d’octobre, on peut utiliser la syntaxe suivante :
model.sales[10].value
Analyse du problème résolu
En récupérant l’ensemble des valeurs optimisées des variables, on obtient le tableau suivant :
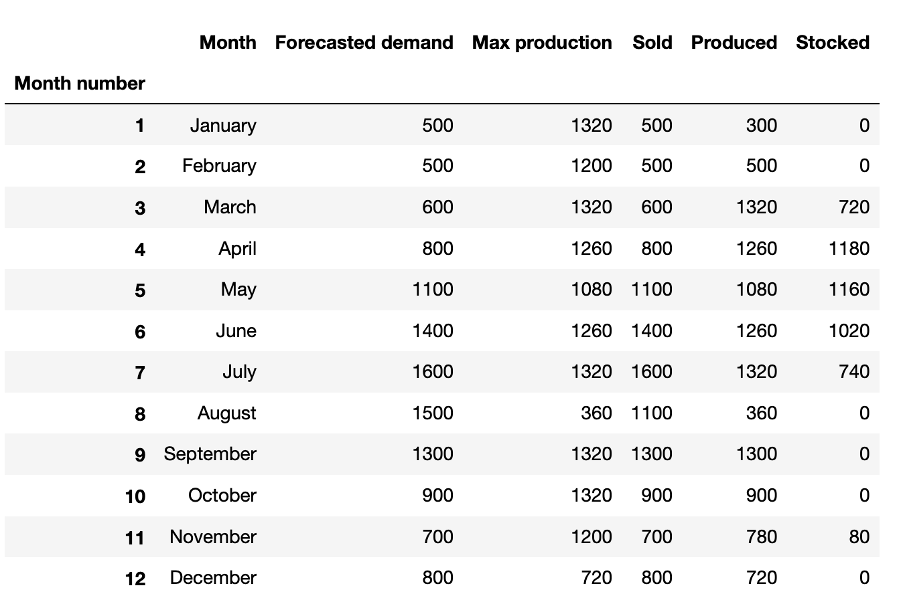
On remarque ainsi par exemple que l’algorithme a évalué qu’il n’était pas intéressant de faire des stocks durant les mois de janvier et février alors qu’en août les quantités de ventes prévues n’atteignent pas la demande estimée. En effet, produire un T-shirt en février et le vendre en août aurait un coût total de 10,6€ (4€ + 1,1€ x 6), ce qui dépasse le prix de vente de 10€. La production étant déjà à saturation entre mars et août, l’importante demande client du mois d’août n’est donc pas satisfaite.
Le problème détaillé ici était très simplifié : l’entreprise ne vend qu’un seul produit, à un prix unique et un coût de production unique. Un problème réel sera généralement bien plus complexe. Néanmoins,une démarche similaire à celle introduite dans l’article peut être appliquée pour de nombreuses entreprises.
Pour aller plus loin
Un problème réel plus complexe pourra nécessiter davantage de temps de calcul : le choix du solveur et son paramétrage devient alors bien plus important que dans notre exemple.
Par ailleurs, le problème que nous avons étudié était un problème linéaire. En effet, chaque terme, de chaque contrainte et de la fonction objectif, était soit une constante, soit le produit d’une variable et d’une constante. À l’inverse, si un terme avait été constitué d’un produit de variables, le problème aurait été non-linéaire. Dans ce cas, CBC n’est pas en mesure de résoudre le problème. D’autres solveurs pourront potentiellement résoudre le problème, comme Bonmin ou Couenne par exemple.
Alternatives à Pyomo
Pyomo n’est pas la seule bibliothèque d’optimisation sous contraintes utilisable avec Python. On peut également citer Google OR-Tools, PuLP, scipy.optimize, CVXOPT ou encore mlrose. Chaque bibliothèque dispose de ses propres spécificités, mais Pyomo reste cependant souvent un bon compromis car elle permet de résoudre un grand nombre de problèmes d’optimisation en gardant une syntaxe simple.

