Détection d'anomalies dans les séries temporelles

[latexpage]
Savez-vous comment une banque détecte automatiquement l’utilisation malveillante des cartes bancaires et vous informe que votre carte a été volée ? Ou bien comment un robot de trading décide si un changement soudain du prix des actions est le début d’une tendance, ou s’il s’agit simplement d’un événement soudain et que le prix va revenir à la normale ? Ces sujets, et de nombreux autres, sont des cas de détection d’anomalies dans les séries temporelles.
Les séries temporelles sont l’un des sujets majeurs des statistiques et de la Data Science. On les rencontre dans une grande variété de contextes : ventes d’une entreprise, transactions bancaires ou le nombre des cas du Covid-19.
Elles sont représentées par une suite de valeurs indexées par le temps. Les observations sont auto-corrélées, ce qui signifie que les observations sont fortement liées à celles qui les précèdent. Les données de séries temporelles doivent être traitées d’une manière particulière en raison de ces contraintes.
D’autre part, les anomalies sont des observations rares ou qui ne suivent pas la distribution des données attendue. La détection des anomalies est un sujet fondamental dans de nombreuses applications, dans les transactions financières, ou bien dans le domaine de la sécurité des réseaux.
Venons-en maintenant au sujet en question, la détection des anomalies dans les séries temporelles. En premier lieu nous parlerons des raisons pour lesquelles la détection d’anomalies est importante, ensuite nous discuterons les techniques utilisées. Ces techniques peuvent être regroupées en deux catégories : l’approche statistique et l’approche du Machine Learning.
Pourquoi utiliser l’intelligence artificielle dans la détection des anomalies ?
L’utilisation d’algorithmes d’IA pour la détection d’anomalies a principalement trois intérêts :
- La première est qu’elle réduit le temps de détection et de correction des anomalies, puisque les algorithmes sont beaucoup plus rapides que les humains, le temps de détection sera donc réduit et peut-être, le problème résolu avant que les clients ne s’en aperçoivent.
- Deuxièmement, il aide à la détection d’anomalies qui ne sont pas détectable par les humains, certaines anomalies sont faciles à détecter, mais d’autres sont beaucoup plus difficiles à repérer. Exemple : Dans le contexte de la cybersécurité, un logiciel malveillant peut être exécuté dans l’ordinateur d’un utilisateur particulier et se mettre à rechercher des données sensibles auxquelles il a accès. Bien que cela puisse être considéré comme un comportement normal parce que l’utilisateur a accès à ces données, l’IA peut considérer que c’est anormal en comparant ce comportement au comportement antérieur de l’utilisateur.
- Troisièmement, elle peut aider à comprendre la cause des anomalies et à prendre de meilleures décisions pour en réduire l’impact. Il est possible que certaines anomalies se produisent fréquemment en raison de causes inconnues.
Les types d’anomalies
Les anomalies peuvent être classées en trois types, et il est important de savoir à l’avance quel type d’anomalie est présent dans les données, cela permet de sélectionner les meilleures méthodes de traitement, et donc de rendre les résultats plus fiables.
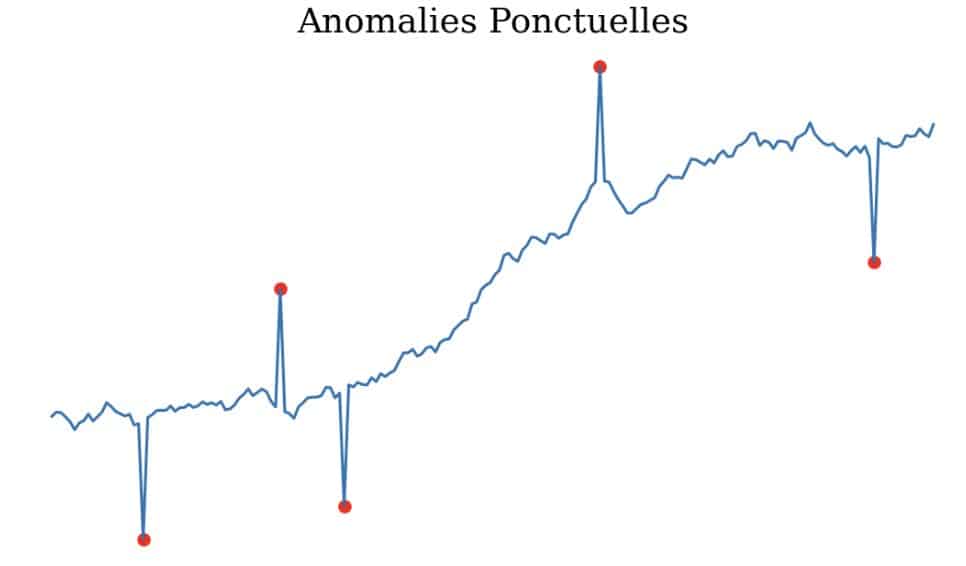
Anomalies ponctuelles : Il s’agit d’une anomalie qui s’écarte de manière significative de la distribution des données ponctuellement, elle peut être un pic ou un creux. Elle peut être détectée en la comparant soit aux autres valeurs de la série temporelle (valeur aberrante globale), soit à ses points voisins (valeur aberrante locale). Exemple : Une transaction de crédit qui diffère des autres transactions dans ses caractéristiques telles que le montant de la transaction et le pays ou la transaction a été effectuée.
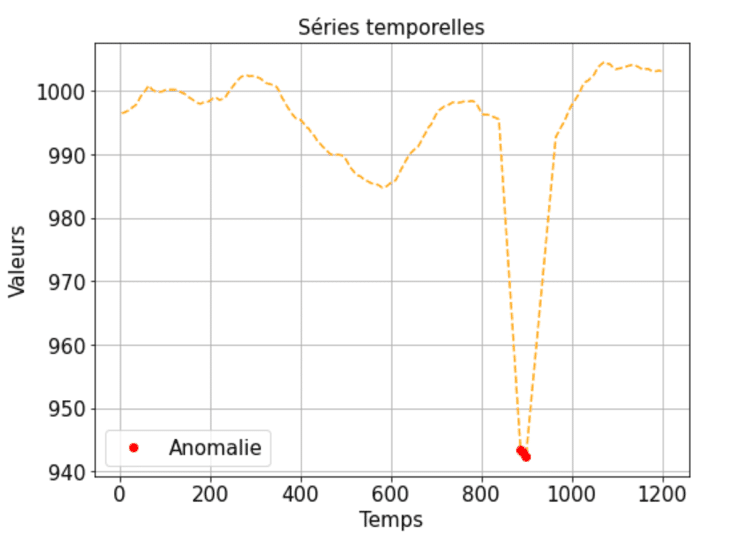
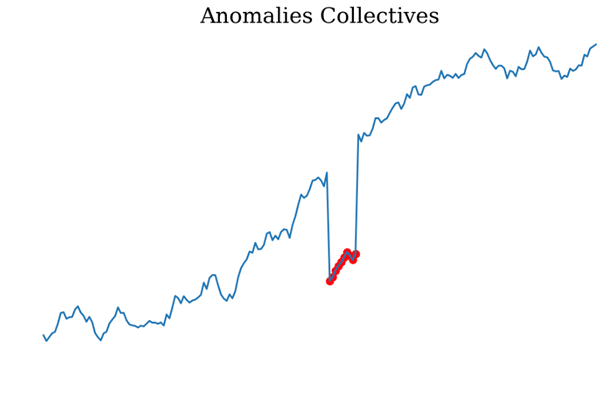
Anomalies collectives : Il s’agit de suites consécutives de points qui s’écartent de manière significative de la distribution jointe, bien que chaque observation prise individuellement ne soit pas nécessairement une anomalie. Exemple, supposons qu’une cliente d’une banque effectue 7 fois des achats avec sa carte bancaire dans la même heure et pour le même montant de 60 €. Bien qu’un achat occasionnel de 60 € soit normal pour la cliente, une série d’achats avec les mêmes caractéristiques et le même montant est inhabituelle.
Anomalies contextuelles : Certains points peuvent être normaux dans un contexte mais anormaux dans un autre. Par exemple : Une température quotidienne de 35 C en été est considérée comme normale en France, alors que la même température en hiver est considérée comme anormale.
Dans cet article, nous nous concentrons sur les techniques de détection d’anomalies ponctuelles et contextuelles.
Techniques de détection d’anomalies dans les séries temporelles
Dans cette partie, nous abordons les méthodes utilisées pour la détection d’anomalies ponctuelles dans les séries temporelles. Les techniques sont divisées en deux catégories, la première est l’approche statistique, où nous supposons que les données sont générées par un processus stochastique, la seconde sont les méthodes Machine Learning, où nous traitons le processus de génération des données comme une boîte noire et essayons d’apprendre uniquement à partir des données.
Illustrons ces approches avec un exemple. Nous allons analyser le nombre de demandes de taxi par heure à New York. Détectons les heures anormales.
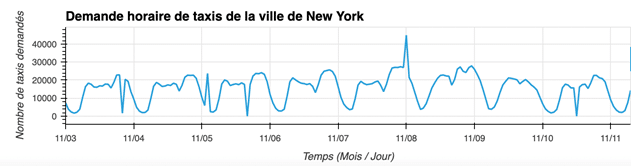
Approches statistiques
Intuitivement, une anomalie est une observation qui s’éloigne du trafic normal. On peut classer une observation comme anormale si elle est suffisamment éloignée du trafic et de l’activité normale.
Une façon de détecter les anomalies dans les séries temporelles est d’estimer la valeur attendue ou le trafic normal et de la comparer à la valeur réelle en utilisant une distance. Une observation est considérée comme une anomalie si la distance à sa valeur attendue est supérieure à un seuil prédéfini.
Il existe plusieurs méthodes pour estimer la valeur attendue, l’une d’entre elles consiste à utiliser des mesures statistiques telles que la médiane ou la moyenne, ces mesures étant calculées globalement ou localement. La différence entre la valeur réelle et la mesure statistique est utilisée pour détecter l’anomalie.
Une autre approche statistique est la modélisation probabiliste, dans laquelle nous supposons que la série temporelle peut avoir une représentation simplifiée, en termes d’équations ou de fonctions, de sorte que ce modèle est supposé représenter l’état normal du trafic.
Dans ce cas, pour détecter les anomalies, un modèle est sélectionné, et ses paramètres sont ajustés à la série temporelle. Comme indiqué précédemment, les différences entre les valeurs réelles et celles prévues par le modèle sont utilisées pour détecter les anomalies.
Il existe de nombreux modèles statistiques qui peuvent être utilisés : décomposition STL, ARIMA, et régression linéaire…
Décomposition STL
Seasonal-Trend decomposition using LOESS (STL) est une méthode robuste de décomposition des séries temporelles souvent utilisée pour faire des analyses économiques et environnementales. Elle consiste à décomposer une série temporelle en trois composantes : la tendance, la saisonnalité et le bruit.
Dans un premier temps, on peut modéliser la série temporelle en utilisant la décomposition STL, la tendance plus la saisonnalité sont supposées représenter le trafic normal. Puis on analyse le bruit restant, en le comparant à un seuil : si le bruit est supérieur à un seuil c’est une anomalie.
Commençons par décomposer le signal en tendance, saisonnalité, et résidu :
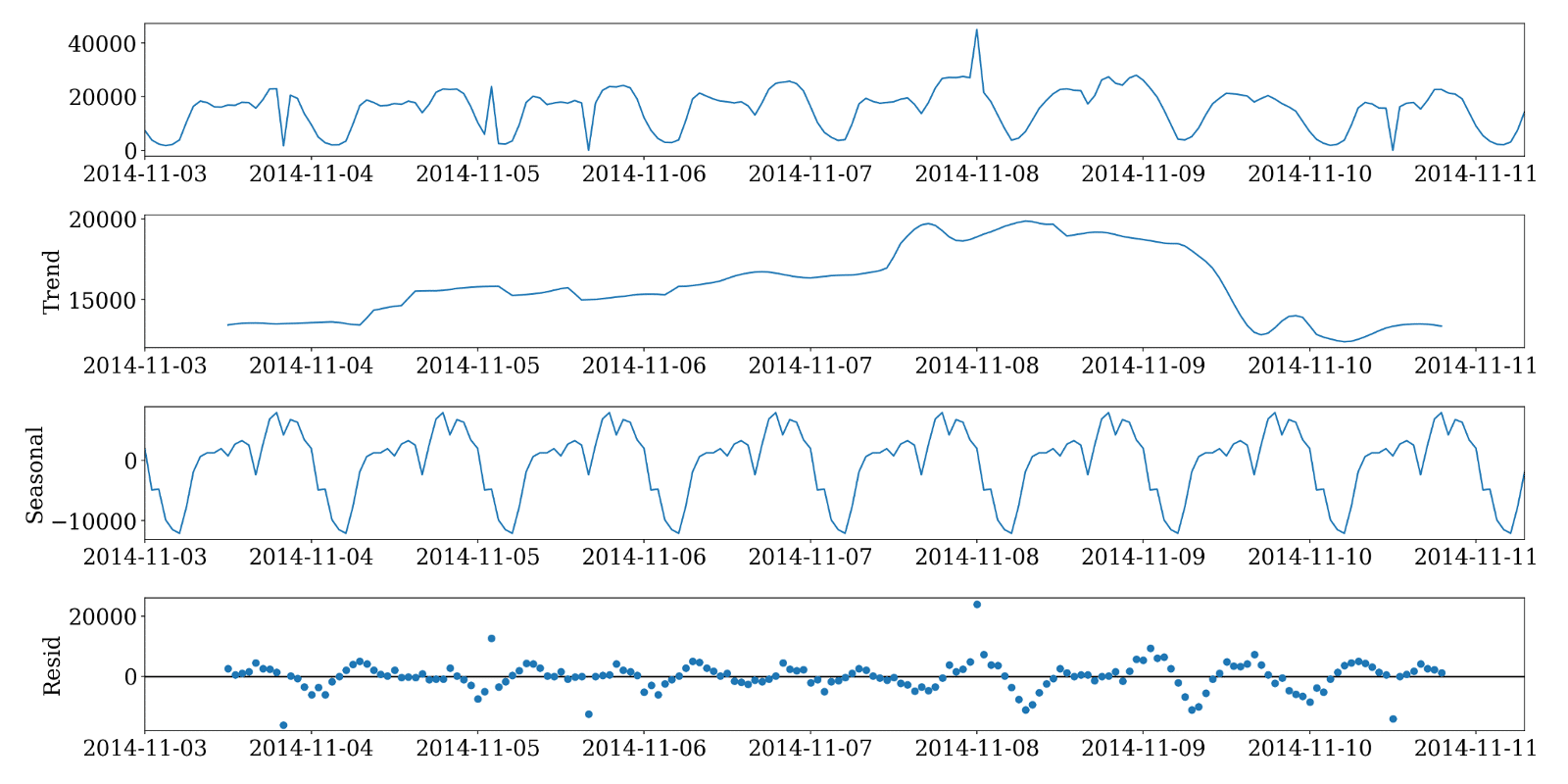
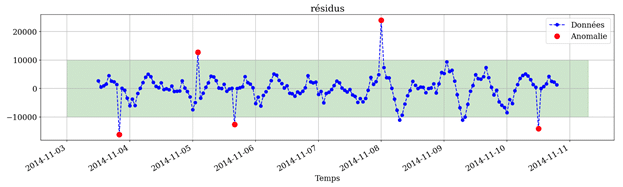
Après avoir éliminé la tendance et la saisonnalité, il suffit d’analyser le résidu pour déterminer quelles sont les observations anormales. Plus concrètement, les résidus en valeur absolue qui dépassent un certain seuil correspondent à des observations anormales.
Ce seuil peut être déterminé suivant des enjeux métier. Dans notre cas, nous supposons que les résidus suivent une distribution normale, donc le seuil peut être déterminé en utilisant le test de Grubb : on considère l’observation comme anormale si la valeur absolue du résidu est supérieure à deux écarts-types
\[
\mu = 0 \text{ et } \sigma = 5000 \\
\mu = 0 \text{ et } \sigma = 5000 \\
\mu = 0 \text{ et } \sigma = 5000 \\
\text{, donc les seuils sont } 10000 \text{ et } -10000.
\]
ARIMA et SARIMA
ARIMA (Autoregressive Integrated Moving Average) est un modèle d’analyse statistique, il explique une série temporelle suivant ses propres valeurs passées, de sorte que ce modèle peut être utilisée pour prévoir les valeurs futures.
Un élément clé d l’analyse des séries temporelles est la stationnarité, autrement dit que les propriétés (espérance, variance, auto-corrélation) d’une observation ne varient pas dans le temps. ARIMA utilise la différenciation des observations (soustraction d’une observation de l’observation précédent) afin de rendre la série temporelle stationnaire et supprimer les tendances.
ARIMA consiste en une combinaison de 3 modèles :
- Auto-régression : Utilise les observations précédentes pour prédire les valeurs futures.
- Intégration – représente toute différenciation qui doit être appliquée afin de rendre les données stationnaires.
- Moyenne mobile – Utilise les erreurs de prévision précédentes plutôt que les valeurs précédentes pour prévoir les valeurs futures.
Bien que la méthode puisse traiter des données avec une tendance, elle ne prend pas en compte les séries chronologiques avec une composante saisonnière.
Une extension d’ARIMA qui prend en charge la modélisation directe de la composante saisonnière de la série est appelée SARIMA.
Comme précédemment, nous allons d’abord chercher le modèle SARIMA qui correspond le mieux à la série temporelle, puis nous identifions les observations anormales en mesurant la distance entre les données réelles et la courbe du modèle (traffic normal).
La différence entre ces modèles et ceux des sections précédentes est que, afin de prédire la valeur attendue (trafic normal) de chaque observation, seules les valeurs précédentes de la série temporelle seront utilisées.
Une limite de cette approche est que les modèles vont essayer de reproduire les valeurs passées. Par exemple, dans l’image ci-dessous, le modèle a appris à reproduire le pic du 11-05, et puis il fait des faux positifs le jour suivant ! Il serait nécessaire de détecter itérativement les anomalies et de ré-entraîner le modèle sur des données non aberrantes.
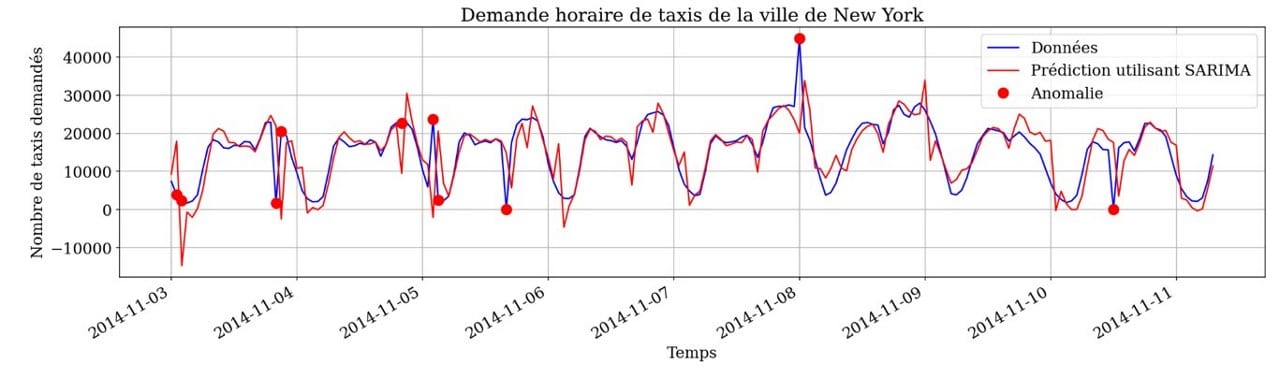
PCA et RPCA
L’analyse en composantes principales (PCA) est une technique statistique non supervisée utilisée pour examiner les relations entre un ensemble de variables et réduire la dimensionnalité, elle décompose une matrice de données en vecteurs appelés composantes principales.
La PCA peut être utilisée pour trouver des données anormales en utilisant l’erreur de reconstruction.
Ceci est réalisé en utilisant les étapes suivantes :
1- Décomposer la matrice des données sources en ses composantes principales.
2- Reconstruire les données originales en utilisant uniquement les premières composantes principales.
3- Les données reconstruites seront similaires, mais pas exactement identiques, aux données originales. Les éléments des données reconstruites qui sont les plus différents des éléments originaux correspondants sont des éléments anormaux.
Bien que la PCA soit une technique bien connue de réduction des dimensions. La PCA classique est basée sur la moyenne empirique et la matrice de covariance des données, et est donc fortement affectée par les observations aberrantes, car elle adaptera ses résultats pour s’ajuster aux observations aberrantes, et donc les considérer comme normales. Il est donc nécessaire de disposer d’une version plus robuste de PCA.
La RPCA (Robust Principal Component Analysis) approxime les matrices de données en une matrice de rang bas d’une manière qui est bien moins sensible aux valeurs extrêmes. Plus concrètement, le RPCA sépare une matrice en la somme d’une matrice de rang bas et d’une matrice d’erreurs creuse.
Approches machine Learning
Les méthodes d’apprentissage automatique tentent d’apprendre uniquement à partir des données et traitent le processus de génération des données comme une boîte noire. Contrairement aux approches statistiques précédentes qui supposent généralement que les données sont générées par un modèle statistique spécifique.
Dans cette catégorie, on distingue principalement deux types d’approches dans le traitement des séries temporelles.
Supervisé
Les techniques formées en mode supervisé ont besoin d’un ensemble de données d’apprentissage avec des instances étiquetées pour les classes de normalité et d’anomalie.
Dans ce cas, une approche courante consiste à créer un modèle prédictif pour les classes normales et les classes d’anomalies. Toute instance de données précédemment non vue est comparée au modèle pour déterminer à quelle classe elle appartient.
Dans la détection supervisée des anomalies, deux problèmes majeurs se posent :
Premièrement, les instances anormales dans les données d’apprentissage sont beaucoup moins nombreuses que les instances normales, ainsi on se trouve face au problème des données déséquilibrées.
Deuxièmement, il est généralement difficile d’obtenir des “labels” précises et représentatives, en particulier pour la classe des anomalies.
Non-supervisé
L’apprentissage non supervisé diffère de l’apprentissage supervisé en ce qu’il tente de découvrir une structure latente dans des données non étiquetées. Comme ces stratégies ne nécessitent pas de données de formation étiquetées, elles sont les plus utilisées.
Les stratégies de cette catégorie partent de l’hypothèse implicite que les occurrences normales dans les données de test sont beaucoup plus fréquentes que les anomalies. Si cette hypothèse est incorrecte, ces systèmes ont un taux élevé de fausses alarmes. En effet, taux de contamination doit être estimé à partir des données réelles, et dans certains modèles, il présente un paramètre d’entraînement (ex : Isolation Forest).
Il existe de nombreuses approches dans la détection d’anomalies non supervisées. Nous avons sélectionné deux méthodes avec des approches différentes.
Ces méthodes ne s’appliquent pas uniquement aux séries temporelles, donc pour les appliquer aux séries temporelles, un prétraitement des données est nécessaire. Par exemple : il faut d’abord rendre la série temporelle stationnaire, et ce en supprimant la tendance et la saisonnalité, dans le cas contraire, des nouveaux points avec une tendance croissante risquent d’être classés comme anomalies. En outre, l’ajout des features temporelles peut améliorer leurs performances, comme les moyennes et les variances glissantes.
Isolation Forest
L’objectif de la forêt d’isolation est de d’isoler les anomalies des points normaux. Ceci est accompli en utilisant des arbres binaires pour partitionner les données.
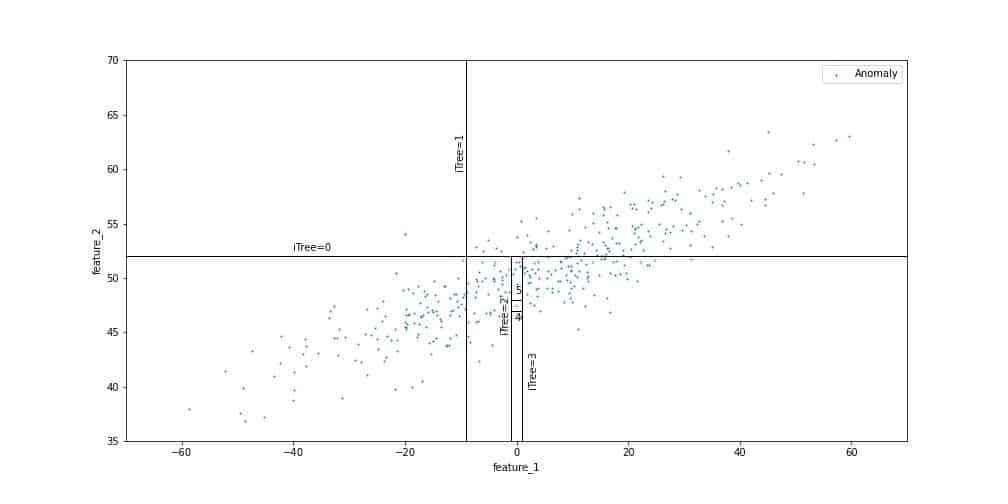
Les arbres séparent l’espace de manière aléatoire jusqu’à ce que chaque observation soit isolée. On détermine ensuite le nombre de séparations nécessaires pour chaque observation, autrement dit la profondeur de la feuille correspondante dans l’arbre binaire. En effet, les observations solitaires nécessitent moins de séparations que les autres. Dans l’exemple ci-dessous, l’isolation du point éloigné de la distribution des données, labélisé comme une anomalie, n’a nécessité que deux partitions. En revanche, isoler un point faisant partie de la zone peuplée des données requiert plus d’étapes.
Ce processus est répété plusieurs fois, définissant à chaque fois un nouvel arbre binaire. Le score d’anomalie de chaque observation est calculé comme le nombre moyen de séparation qui ont été nécessaire pour l’isoler dans chaque arbre.
Clustering
Il s’agit de regrouper les données en clusters (groupes de données similaires selon une métrique choisie par l’algorithme). L’anomalie sera évaluée dans le cas de données qui ne peuvent être regroupées et qui sont situées loin des données regroupées.
Le clustering K-means est une approche de clustering typique de cette catégorie. En appliquant cet algorithme, les points de données sont regroupés en K clusters. Lorsque les échantillons de données ont des valeurs de caractéristiques comparables selon une fonction de distance spécifique, ils seront regroupés au sein du même cluster. Enfin, la distance au centroïde du cluster est utilisée pour calculer le score de chaque point de données. Les anomalies sont des points de données qui sont situés loin du centroïde du cluster.
Pour ces deux méthodes, on ajoute souvent des features pour prendre en considération le contexte temporel. Par exemple, en ajoutant la différence entre la valeur à l’instant t et celle à l’instant t-1 pour une série donnée, on obtient l’information de la variation de la série, ce qui permettra de détecter les pics et les valeurs extrêmes par exemple.
Conclusion
Félicitations, vous êtes arrivé à la fin ! Vous connaissez maintenant la détection des anomalies dans les séries temporelles. Nous avons expliqué pourquoi il s’agit d’une tâche importante dans différents contextes métiers, et comment exploiter l’IA pour réaliser cette tâche.
Un mot avant de partir, Les données de séries temporelles peuvent varier considérablement selon le cas d’utilisation, et il n’est pas possible de déterminer quelles méthodes sont les meilleures sans prendre en compte les exigences et les objectifs spécifiques de votre analyse. Chez Quantmetry, nous comprenons les avantages et les inconvénients de chaque méthode et pouvons aider nos clients à appliquer la technique la plus adaptée à leur cas d’utilisation spécifique.
La mission de l’expertise Time Series est d’exploiter le potentiel de vos séries temporelles à l’aide de solutions d’IA : analyse des données historiques, prévisions de demande, de parts de marché, de production, détection d’anomalies sur des données IoT.

Data Scientist chez Quantmetry
Diplômé en Data Science de Telecom Paris et Polytechnique Paris, je possède des compétences solides en programmation, apprentissage automatique et statistiques. Ayant travaillé sur divers projets, tels que le minage de texte, systèmes de recommandation, détection d'anomalies et classification d'images, je suis passionné par les avancées en Data Science et motivé à les appliquer dans des initiatives innovantes.

Data Scientist chez Quantmetry
Après avoir été diplômé de l'École des Mines de Paris, j'ai rejoint Quantmetry en tant que Data Scientist. Je m'intéresse à la science des données et à ses applications dans l'industrie. Ainsi, j'ai participé à des missions dans les secteurs de l'énergie et du luxe, où j'ai pu utiliser les données pour aider les clients à résoudre des problèmes opérationnels et commerciaux. Mes passions sont les données et l'apprentissage automatique, et je cherche toujours à apprendre et à découvrir les dernières nouveautés dans ces domaines.