Comment créer des modèles interprétables sans approximation ?

crédit : Lea Kelley
Le développement de l’Intelligence Artificielle a abouti au déploiement de nombreux modèles extrêmement performants mais dont le fonctionnement reste obscur. Ces boîtes noires sont parfois utilisées dans des applications sensibles telles que le recrutement ou l’attribution de prêts. Pour ces applications il est aisé de créer des modèles qui semblent performants mais qui reposent en réalité sur des patterns trompeurs, inacceptables ou biaisés.
Se forger une bonne compréhension des modèles et de leurs prédictions est un bon moyen d’éviter ces écueils. L’interprétabilité des modèles d’IA et de leur prédiction est donc fondamentale pour leur acceptation, et pour éviter la reproduction de biais historiques. Pour obtenir plus d’information sur le comportement des boîtes noires, il est fréquent d’ajouter une couche d’interprétabilité aux solutions déjà déployées reposant sur une approximation plus simple de ces modèles (par exemple en utilisant Shap et ses valeurs de shapley). Cependant comme indiqué, l’interprétabilité repose alors sur une approximation du modèle et est donc imparfaite. Nous explorons dans cet article une autre solution consistant à prendre en considération l’interprétabilité des modèles dès leur conception sans avoir à faire appel à une approximation.
Comment inclure la compréhension humaine dès la conception d’un modèle ?
Lors du Neural Information Processing Systems (NeurIPS) 2018, Lage et al. ont proposé un cadre pour prendre en considération l’interprétabilité dès la conception des modèles. Ils proposent basiquement de considérer beaucoup de modèles plausibles et de les sélectionner a posteriori. Le critère de sélection proposé est alors une combinaison de la performance du modèle et de son interprétabilité.
Les auteurs proposent une méthode pour évaluer l’interprétabilité des modèles. Elle consiste à fournir la structure du modèle à un humain pour qu’il reproduise les prédictions du modèle. Le temps de réponse est ensuite utilisé pour estimer l’interprétabilité du modèle. Cette méthode étant peu adaptée à des modèles très complexes, ils proposent, dans ce cas, de calculer plusieurs approximations plus simples en perturbant les données autour du point à prédire. Ces approximations sont alors soumises à l’étude d’interprétabilité décrite précédemment. L’interprétabilité du modèle complexe est alors la moyenne de l’interprétabilité des approximations locales.
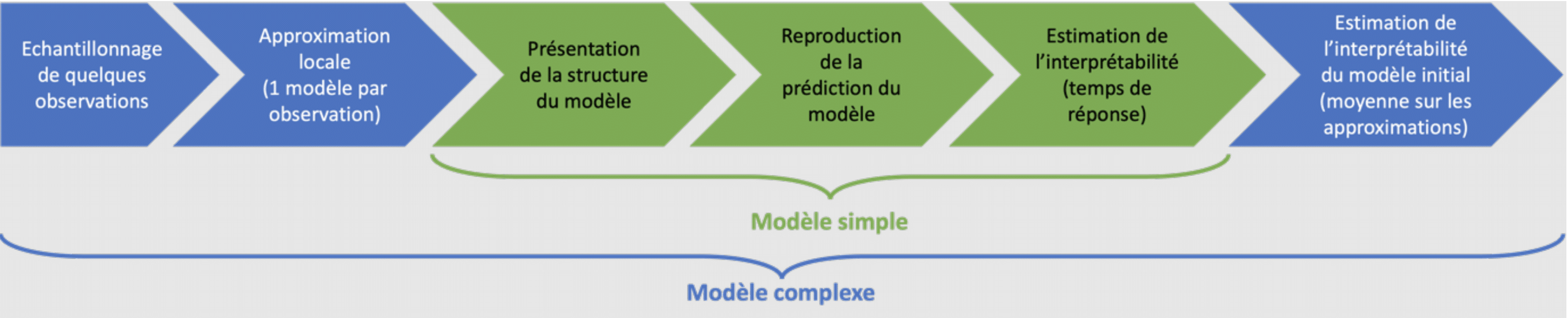
Figure 1 : Process d’évaluation de l’explicabilité d’un modèle
L’étude du niveau d’interprétabilité des modèles est clairement l’étape la plus longue du processus de sélection. Les auteurs ont donc proposé deux façons de réduire le nombre de modèles à étudier : n’étudier que les modèles les plus performants et modéliser l’interprétabilité des modèles en ne réalisant d’étude que pour quelques modèles choisis aléatoirement parmi ceux-là.
Comment éviter l’étude d’interprétabilité des modèles ?
L’étude de l’interprétabilité des modèles est la tâche la plus coûteuse de la méthode précédemment décrite. Il est donc parfois préférable de choisir dès le départ un modèle interprétable par design. Cette section présente certains de ces modèles.

Figure 2 : Les aspects de l’intelligibilité en IA
| Type de modèle | Avantages | Inconvénients | |
| Blackbox + interprétabilité | Performances | Temps de calcul élevé
Approximation d’un premier modèle |
|
| Régression Linéaires et Modèles Linéaires Généralisés | Interprétabilité
Vitesse de calcul |
Performances
Nécessite de spécifier les interactions |
|
| Modèles Additifs Généralisés | Interprétabilité
Performances |
Difficulté à sélectionner les transformations non linéaires | |
| Arbres de classification et de régression | Interprétabilité
Vitesse de calcul |
Performances (variance)
Difficulté à décrire des relations linéaires |
|
| Règles de décision | Interprétabilité
Concision |
Performances
Difficulté à décrire des relations linéaires |
|
| SkopeRules | Interprétabilité | ||
| Rulesfit | Interprétabilité | Performances | |
| RiskSlim et Modèles Parcimonieux d’Entiers | Interprétabilité | Temps de calcul potentiellement élevé | |
| Classifieur de Bayes | Interprétabilité | Hypothèse d’indépendance des variables | |
| Réseaux Bayésiens | Performances
Interprétabilité (si peu de variables) |
Perte rapide d’interprétabilité
Temps de calcul et difficulté à trouver la structure du réseau |
|
| Table récapitulative des modèles interprétables | |||
Les modèles linéaires : comment obtenir des modèles sous forme d’une somme ?
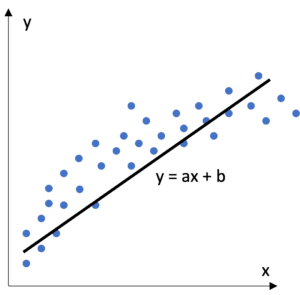
Figure 3 : Régression Linéaire
Les modèles de régression linéaire reposent sur la somme pondérée des variables passées en entrée. Pour une variable continue (par exemple : la taille, le revenu mensuel) issue d’un ensemble de variables ayant la même échelle, le poids associé peut être facilement interprété comme l’importance de cette variable pour le modèle. Ainsi une augmentation de 1 de la variable induit une augmentation la sortie du modèle du poids associé à la variable. Pour une variable catégorielle (par exemple : le département de résidence d’un client), la valeur 0 est attribuée à une catégorie de référence et les autres catégories prennent la valeur 1 quand elles sont rencontrées et 0 quand une autre catégorie est rencontrée. Le poids associé est donc directement l’effet de la catégorie sur la sortie du modèle.
Ces modèles sont très adaptés pour donner des prévisions sur des variables continues (comme un prix ou un nombre de ventes). Les limitations connues sont :
- La prédiction des catégories (comme le décrochage d’un client), qui doit prendre des valeurs entre 0 et 1
- La prédiction de très petites quantités strictement positives (comme le nombre attendu de défauts d’un type d’équipement sur une période d’un mois), pour lesquelles ces modèles peuvent prédire des valeurs négatives.
C’est pourquoi ces modèles ont été étendus pour couvrir plus de cas d’usages, on parle de modèles linéaires généralisés (GLM). Cette généralisation utilise une fonction mathématique pour adapter la sortie d’une régression linéaire à ces cas particuliers
Plus précisément on parle de régression logistique pour la classification. La sortie est alors la probabilité d’appartenir à la classe cible. Les poids sont interprétables comme des déplacements de la probabilité vers ou hors de la classe cible.
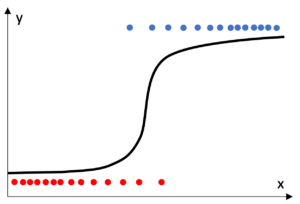
Figure 4 Régression logistique
Pour les valeurs strictement positives on parle de modèles log-linéaires. La sortie du modèle est alors log transformée pour prendre des valeurs potentiellement négatives. Un effet de cette transformation est le passage du modèle de la forme d’une somme à celle d’un produit. Les poids sont alors interprétables comme une correction en puissance de l’effet des variables sur la sortie.
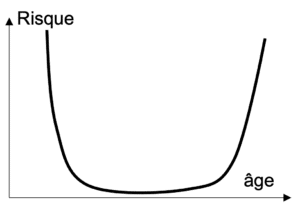
Figure 5 : Relation non linéaire entre l’âge et le niveau de risque
Enfin, l’effet d’une variable n’est pas forcément linéaire. Par exemple pour calculer le montant d’une prime d’assurance il n’est pas forcément judicieux de faire augmenter le prix avec l’âge de l’assuré (comportement linéaire). En effet, les personnes plus jeunes ont des conduites plus à risque donc le montant de la prime pourrait être augmentée pour compenser cette tendance. Dans ce cas, le montant devrait décroître avant de réaugmenter avec l’âge (comportement non linéaire). Cette situation est fréquemment rencontrée, pour cette raison des modèles intégrant des transformations non linéaires des variables ont été développés. On parle alors de modèles additifs généralisés (GAM). Parmi les GAM on compte par exemple les régressions par spline, et le nouvel algorithme de machine à boosting explicable (EBM).
Si tous ces modèles ont une forme facilement interprétable, l’accumulation de transformations et de variables en rend l’interprétation de plus en plus difficile. Ces modèles sont donc d’autant plus interprétables qu’ils comprennent peu de variables.
Arbres et règles de décision : comment mieux gérer les interactions entre variables ?
Les modèles linéaires et additifs peuvent être utilisés dans de nombreuses situations mais sont peu performants quand les variables interagissent entre elles. Les modèles reposant sur des arbres de décision n’ont pas ce problème.
Un arbre divise le jeu de données en deux selon une certaine valeur seuil pour une variable. Chaque division est un alors un nœud de l’arbre dont sont issue deux branches. Les extrémités des dernières branches sont les feuilles de l’arbre. L’algorithme de création d’arbre le plus courant est l’algorithme d’arbre de classification et de régression (CART).
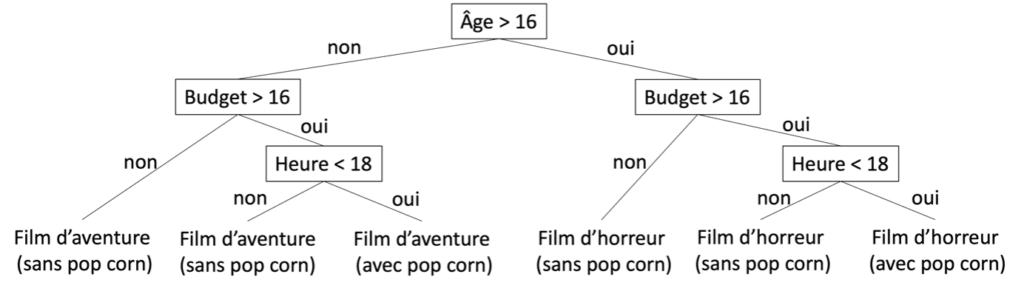
Figure 6 : Arbre de décision pour une sortie au cinéma
Par multiples divisions successives, un arbre peut retrouver des groupes d’observations dans le cadre d’un problème de classification. Dans le cadre d’un problème de régression, on attribue à chaque feuille la moyenne des valeurs observées pour ce groupe dans les données d’entraînement. D’une manière intéressante, la formation des groupes ne nécessite pas de transformation des variables.
L’interprétation des arbres de décision est simple. En commençant à la racine (avant la première division), il suffit de suivre la structure de l’arbre jusqu’à une feuille. Chaque nœud donne une condition pour appartenir au groupe de la feuille. L’ensemble des conditions est lié par un ET logique, par exemple : si âge supérieur à 16 ET budget supérieur à 16 euros ET heure inférieure à 18, l’observation appartient au groupe qui va voir un film d’horreur et achète du pop-corn.
Les règles de décision peuvent être vues comme une extension des arbres de décisions. Il s’agit d’une structure de la forme « SI condition 1 ET condition 2 OU condition 3 ALORS conclusion ». Les règles de décision sont aussi expressives que les arbres, tout en étant plus concises et facilement intelligibles. En effet, pour être équivalent à une seule règle de décision, un arbre peut contenir plusieurs fois la même séparation qui serait répétée dans plusieurs sous arbres. Par exemple, dans l’arbre décrit précédemment les séparations « Budget » et « Heure » sont répétées. Il est facile d’arriver aux même séparations en utilisant deux règles : « SI Budget > 16 ET Heure < 18 ALORS avec pop-corn » et « SI Âge > 16 ALORS Film d’horreur ».
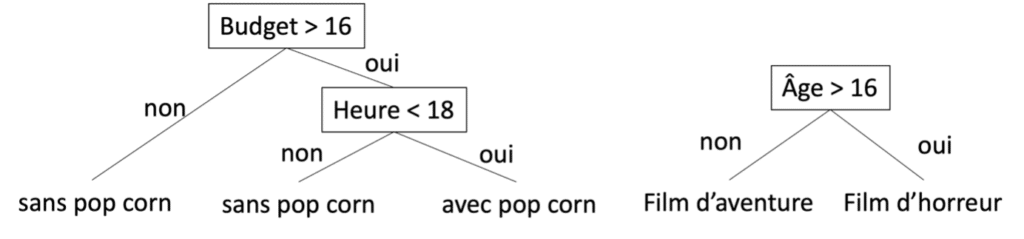
Figure 7 : Règles de décision pour une sortie au cinéma
Les algorithmes de construction de règle se concentrent généralement sur des problèmes de classification. Les plus fréquents sont des variantes de l’algorithme de Sequential Covering qui repose sur un calcul d’arbre. La règle est alors calculée en parcourant l’arbre jusqu’à la feuille qui isole la plus grosse fraction possible du jeu de données, et en appliquant la méthode d’interprétabilité décrite précédemment. Les points contenus dans la feuille sont alors retirés et l’opération est répétée de manière séquentielle jusqu’à avoir isolé tous les groupes cibles.
Là encore si la forme des arbres et des règles est très facilement interprétable, la multiplication des variables complique la lisibilité de ces modèles. De plus, ces modèles de machine learning décrivent mal les relations linéaires.
RuleFit et SkopeRules : Comment concilier les avantages des modèles linéaires et des arbres ?
Rulefit est un algorithme qui tente de palier les limitations des modèles linéaires, qui représentent bien les relations linéaires entre les variables mais pas les interactions, et des arbres, qui représentent bien les interactions entre variables mais mal les relations linéaires. L’idée est de calculer un modèle linéaire intégrant des règles :
- Les règles sont à nouveau tirées d’arbres eux même calculés de manière à prédire la variable cible (par exemple dans une forêt aléatoire).
- Pour éviter d’accumuler trop d’éléments dans le modèle (variables initiales et règles) le modèle est pénalisé pour que certains coefficients s’annulent ce qui revient à ne pas inclure les variables ou règles associées (pénalité lasso).
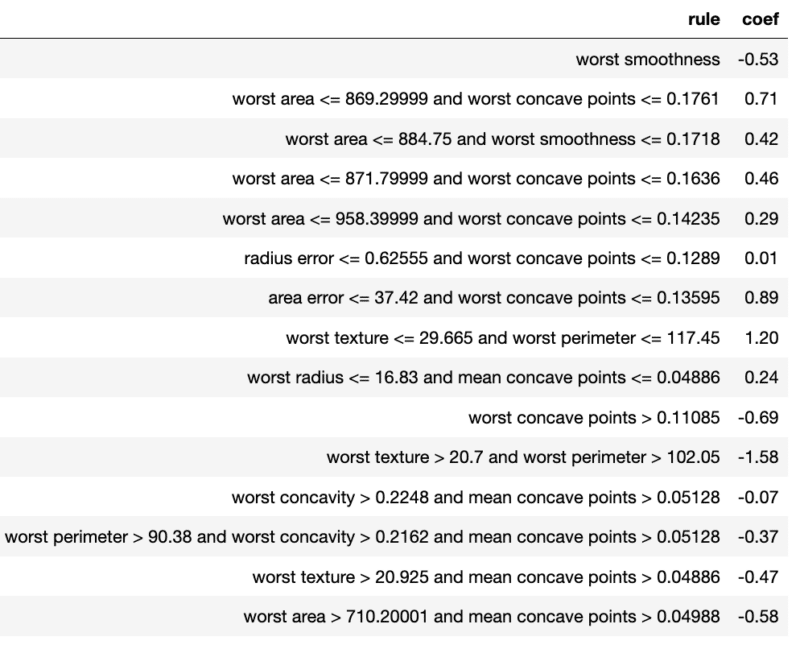
Figure 8 : Exemple de sortie de l’algorithme RuleFit
Le modèle est facilement interprétable comme un modèle linéaire, cependant il convient d’ajouter une contrainte sur les règles pour qu’elles ne portent pas sur plus de 2 ou 3 variables. L’ajout de règles ne diminue pas forcément l’interprétabilité du modèle. En effet, toutes les règles ne s’appliquent pas nécessairement à toutes les observations, ce qui permet de simplifier le modèle lorsqu’on s’intéresse à un cas en particulier. Toutefois, des règles qui se recouvrent peuvent être problématiques. En effet, les poids des règles sont calculés « toutes autres variables ou règles fixées ». Or si deux règles se recouvrent, la première s’applique potentiellement lorsque la seconde est applicable, et donc le poids associé à chacune de ses règles est biaisé.
SkopeRules est un autre algorithme qui extrait des règles d’un ensemble d’arbre, mais sans les inclure dans un modèle linéaire. Les règles dupliquées ou redondantes sont ensuite retirées. Comme les algorithmes d’ensemble (boosting, bagging, random forest) laissent la possibilité de calculer les arbres sur des sous parties du jeu de données, SkopeRules associe également une importance à chaque règle. L’importance de chacune des règles est basée sur sa précision quand elle est utilisée sur les données qui n’ont pas été utilisées par l’algorithme d’apprentissage pour calculer l’arbre dont elle est issue.
RiskSlim et Imodels : comment inclure plus de contraintes d’interprétabilité dans les modèles ?
Imodels est un package de machine learning qui rassemblent de nombreux modèles interprétables, parmi lesquels liste de règles et ensembles de règles ajustées avec AdaBoost (boosted rules). Le package propose aussi une implémentation de modèles linéaires d’entiers parcimonieux (sparse linear integer model, ou slim). Il s’agit d’une variante des modèles linéaires qui ne conserve qu’un nombre réduit de variables (pour le côté parcimonieux) en ne leur attribuant que des coefficients entiers (d’où modèle linéaire d’entiers). Ces modèles peuvent être aussi performant que des modèles linéaires moins contraints à condition que l’ensemble des entiers autorisés au modèle soit suffisamment grand.
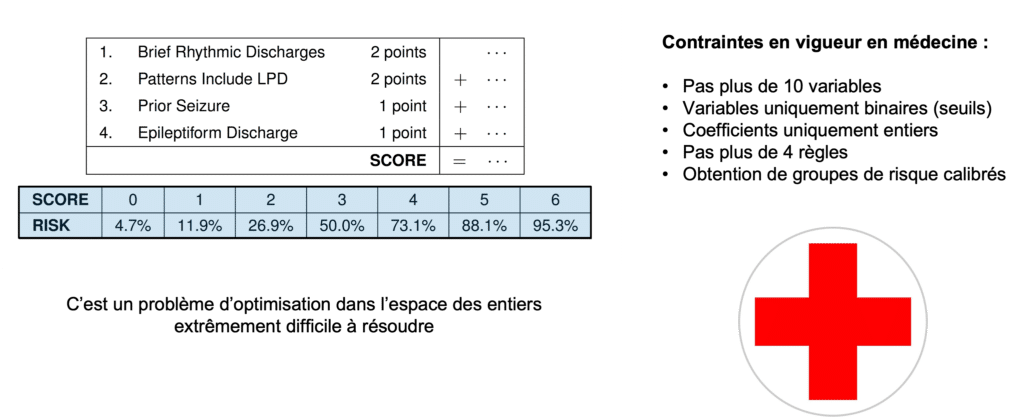
Figure 9 : Les principes de RiskSlim
RiskSlim pousse le concept de modèle linéaire d’entiers parcimonieux plus loin. Le modèle entraîné par RiskSlim prend la forme d’une somme de scores entiers de faibles valeurs (ne dépassant pas 10) associée à un niveau de risque. L’algorithme d’entraînement permet de plus :
- De définir un nombre maximum de variables à inclure
- D’avoir une représentation exclusive des groupes : le modèle s’entraîne en incluant les femmes ou les hommes mais pas les deux ensembles
- De définir le nombre maximum de division à appliquer à une variable catégorielle : par exemple ne créer au maximum que 3 classes d’âge
- D’inclure des structures logiques : par exemple n’inclure l’hypertension que pour les hommes
Le modèle produit est donc facilement compréhensible, puisque ne contenant que peu de variables et uniquement des coefficients entiers. Cependant garantir la qualité prédictive d’un tel modèle est un problème complexe dont le temps de calcul augmente fortement avec la quantité de données à traiter. RiskSlim ne devrait donc être utilisé que lorsque peu de données sont disponibles, par exemple dans le cadre de l’aide au diagnostic médical pour lesquels on ne dispose généralement que des données de quelques dizaines (plus rarement centaines) de patients.
Classifieur naïf de Bayes et Réseaux Bayésiens : comment conserver un modèle interprétable malgré de nombreuses catégories ?
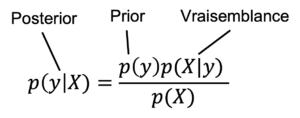
Figure 10 : Théorème de Bayes, la probabilité a postériori (posterior) d’un événement sachant les données est proportionnelle au produit de la probabilité a priori (prior) de l’évènement et de la probabilité des données sachant l’évènement (vraisemblance)
Le classifieur naïf de Bayes utilise les probabilités conditionnelles pour prédire la probabilité d’une observation d’appartenir à la classe cible. Pour chaque observation, cette probabilité est un produit. Le premier membre du produit est la probabilité d’appartenir à la classe cible : c’est-à-dire la proportion de points qui lui appartiennent dans le jeu de données (donc la probabilité a priori d’appartenir à la classe cible). Les autres membres sont les probabilités d’appartenir à la classe cible sachant la valeur de chacune des variables. Ces probabilités, dites conditionnelles, sont elles-mêmes calculées comme le produit de la probabilité d’appartenir à la classe et de la probabilité d’obtenir cette valeur sachant qu’on appartient à la classe (soit la vraisemblance de la valeur). Il est donc possible d’interpréter les probabilités conditionnelles comme des mouvements vers ou hors de la classe cible.
Cependant, le classifieur est appelé naïf car les probabilités conditionnelles sont calculées indépendamment pour chaque variable. Ce mode de calcul implique une hypothèse, dite d’indépendance conditionnelle, qui est une hypothèse forte, très peu souvent vérifiée. Les réseaux bayésiens permettent d’inclure les dépendances conditionnelles dans les calculs. Ces dépendances sont représentées sous la forme d’un graphe qui relie les variables dépendantes et permet donc d’affiner le calcul des probabilités conditionnelles. Toutefois, cette représentation graphique amène deux limitations : 1) plus le nombre de variables augmente, moins le graphe est lisible, 2) déterminer la forme du graphe est souvent un problème extrêmement complexe.
Pour s’assurer de l’interprétabilité d’un modèle il faut appliquer le principe KISS : Keep It Small and Simple
De nombreuses alternatives aux modèles boîtes noires sont disponibles et peuvent d’ores et déjà être utilisées dans les cas où l’interprétabilité du modèle est un élément déterminant. Leur diversité permet de s’adapter à de nombreuses typologies de données. Cependant leur interprétabilité diminue toujours fortement quand le nombre de variables devient très important. Cette limite de notre capacité à intégrer de l’information a déjà été identifiée dans d’autres contextes. Ces observations ont conduit à l’expression de la loi de Miller, une heuristique qui estime qu’un être humain ne peut pas appréhender plus de 7 plus ou moins 2 informations simultanées. La contrainte d’interprétabilité devrait donc pousser fréquemment à choisir des modèles plus simples reposant sur un feature engineering et une sélection des variables idoines. En résumé pour s’assurer de l’interprétabilité d’un modèle il faut appliquer le principe KISS : Keep It Small and Simple.
Bibliographie
Lage I et al. Human-in-the-Loop Interpretability Prior. NeuriPS, 2018
Lou Y. et al. Intelligible Models for Classification and Regression. 2012
Molnar C. Interpretable Machine Learning, A Guide for Making Black Box Models Explainable, 2022
Ustun B. and Rudin C. Learning Optimized Risk Scores. Journal of Machine Learning Research. 2019
Zheng X. et al. DAGs with NO TEARS: Continuous Optimization for Structure Learning. NeuriPS, 2018
Les membres de l’expertise Reliable AI développent des modèles performants, fiables et maîtrisés, sur l’ensemble du cycle de vie, pour une IA de confiance.

Senior Data Scientist
Après avoir automatisé le traitement de données biologiques à haut débit, je me suis tourné vers la Data Science. J’applique aujourd’hui mes connaissances à la construction d’outil de prévision ou d’aide à la décision avec un intérêt particulier pour la fiabilité, l’interprétabilité et la frugalité des modèles.
