DeepFakes et autres générations... Que se cache-t-il derrière les GANs, le prochain game-changer de l’IA ?

[latexpage]

Alors que les applications Zao et FaceApp font l’actualité et suscitent des débats, permettant au choix de s’intégrer dans Game of Thrones à l’aide d’ une seule photo, ou de transformer à l’envie son visage, de nombreux autres cas d’usages impliquant des modèles génératifs se développent.

On peut citer notamment :

• la génération de médicaments, où les modèles génératifs couplés à l’apprentissage par renforcement permettent d’accélérer massivement la synthèse de nouvelles molécules.
• la génération de nouveaux visuels dans le e-commerce : générer une tenue avec un nouveau mannequin, de nouvelles poses, voire un jour décliner à l’infini les possibilités.
• la génération de données médicales synthétiques (ex : Choi et al, 2018) : dans les secteurs à données sensibles, la recherche est prolifique sur les méthodologies permettant de créer des données synthétiques, intéressantes d’un point de vue d’une modélisation Machine Learning. On pense au secteur de la santé, mais également aux entreprises qui ne peuvent historiser les données réelles mais souhaitent historiser des données synthétiques utilisables pour entraîner des modèles (ex : publication de la société Amadeus, Mottini et al. 2018). 
• l’adaptation de domaine visuel : on peut par exemple générer un visuel d’une ville en été, en adaptant à un autre domaine (la même ville mais en hiver, ou encore passer une vidéo tournée de jour en vision de nuit).

Mais d’où vient cette multiplication de succès? 

Réponse courte : des Generative Adversarial Networks (GANs) !

Mais remettons un peu de contexte… Cet article a justement pour objectif d’expliciter les origines de cette méthode, détailler son fonctionnement, ainsi que certaines de ses actualités.

Un modèle… génératif? 

Tandis que le Deep Learning s’illustre depuis plusieurs années par ses performances sur les modèles discriminants (i.e apprendre une représentation complexe entre des données d’entrées de type pixels, mots, sons etc., et des classes ou des valeurs continues), les modèles génératifs profonds étaient jusqu’à récemment encore peu convaincants. Il s’agit d’une classe de modèles non supervisés ayant pour objectif, à partir de données d’entraînement, de générer de nouveaux échantillons provenant de la même distribution. En l’occurrence, on veut générer à partir d’une distribution p_{model} qui soit la plus proche possible de la distribution initiale p_{data}.

Ce problème d’estimation de densité est au coeur de l’apprentissage non supervisé, et s’appréhende de deux façons :

• estimation explicite de densité : on veut explicitement définir p_{model}
• estimation implicite : on veut générer à partir d’une p_{model} ​ de qualité, sans l’expliciter

Goodfellow propose la nomenclature de modèles génératifs suivante :

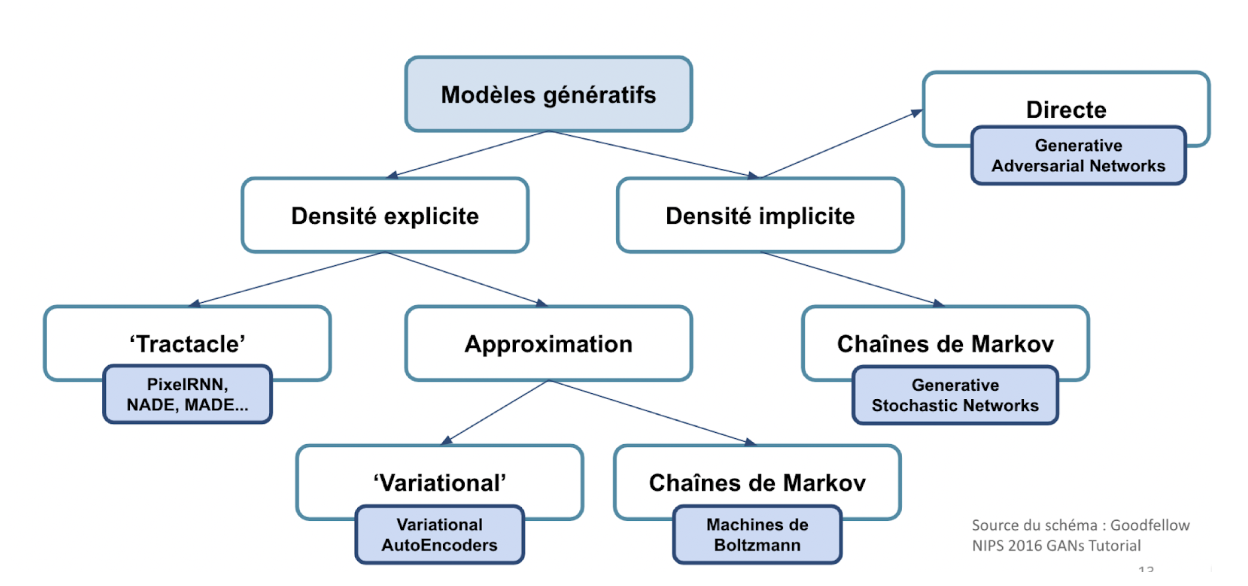
Depuis 2014, et la publication de Generative Adversarial Networks par Goodfellow et al. (plus de 11.000 citations tout de même..), ces méthodologies se sont relancées, avec en particulier l’émergence des réseaux antagonistes génératifs, ou GANs. Il est à noter que les  Variational Autoencoders (VAEs) connaissent également un engouement sur certains cas d’application.

Les GANs sont un cadre d’estimation de modèle génératif. Il s’agit d’une façon d’entraîner des réseaux de neurones à représenter implicitement la distribution qui a permis de générer un certain jeu de données. On peut alors générer de nouveaux échantillons, plus ou moins réalistes selon le niveau de qualité du modèle (on peut dès à présent ouvrir la réflexion sur la façon de qualifier et quantifier cette qualité et ce réalisme !). De façon plus générale, ils permettent d’apprendre une représentation des données de façon non supervisée, qui peut également être utilisée de façon semi supervisée (amélioration de classifieurs sur données asymétriques par exemple par génération de données à labels minoritaires).

Plus précisément, deux réseaux sont entraînés simultanément en concurrence : un générateur G  (responsable de la génération de données, par exemples des images) et un discriminateur D (dans le cadre général, c’est un classifieur quantifiant la probabilité qu’une donnée provienne des données d’origine).

G n’a pas accès aux données d’origine, sa seule façon d’apprendre est via les interactions avec le discriminateur. D a accès aux données d’origine, ainsi que les données dites synthétiques. L’objectif de D est de maximiser la probabilité d’assigner le bon label (réel = 1, synthétique = 0) aux données qui lui sont fournies, réelles et synthétiques. On voit donc qu’on se place dans le cadre classique de la maximisation d’accuracy d’un classifieur. L’objectif de G est quand à lui de maximiser le nombre de données synthétiques labellisées « 1 » par D, donc de tromper D.

Ce cadre correspond à un jeu minimax à deux joueurs, pour lequel une unique solution, un équilibre de Nash, existe sous certaines conditions.

Le “vanilla GAN”, ou GAN d’origine 

Les GANs permettent une grande flexibilité de définitions de fonction objectif et plus généralement d’architecture.

Le générateur des GANs d’origine, ou vanilla GANs minimise théoriquement la divergence Jensen-Shannon entre données réelles et synthétiques, mais de nombreuses reformulations et extensions sont possibles, permettant d’élargir le cadre initial à des données avec discontinuités par exemple (catégorielles etc). Il est en pratique très courant d’adapter le problème d’optimisation avec des critères alternatifs par rapport aux décisions de D. 

Schéma de fonctionnement des vanilla GANs :

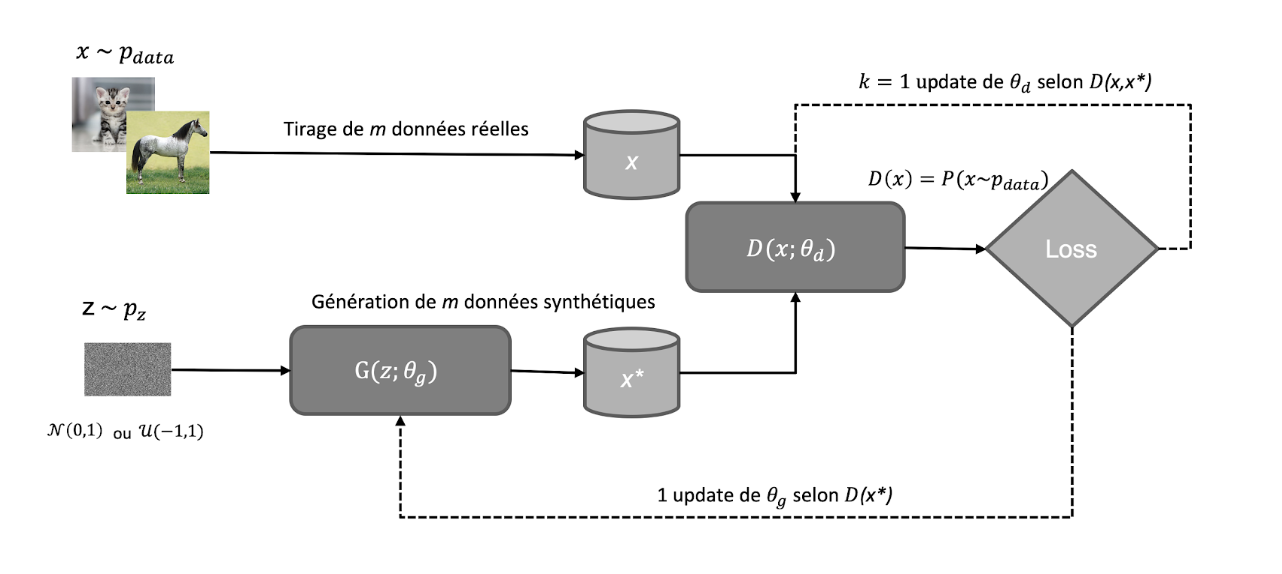
Notations :

• p_{data} ​ : la distribution des données réelles data
• p_{z} : une distribution connue qu’on pourra échantillonner de façon à obtenir un bruit aléatoire z utilisé comme entrant de notre réseau (usuellement gaussien ou uniforme).
• G: z \rightarrow x tel que si z \sim p_z , alors x \sim p_d. G = G(z,\theta_g) un réseau de neurones de paramètres g .
• D: x \rightarrow y \in (0,1)  où y est la probabilité estimée que x provienne de p_{data}​​. D = D(x,\theta_d)un réseau de neurones de paramètres d .

On entraîne D pour maximiser la probabilité d’assigner un label correctement (que ce soit pour un exemple du dataset ou venant de G ) . En parallèle, on entraîne G pour minimiser log(1-D(G(z)))  c’est-à-dire que l’on souhaite que D(G(z))  soit le plus proche de 1 (donc que le discriminant se “trompe” et classifie notre exemple comme venant du dataset). 

On obtient alors la fonction objectif suivante :

\min_{G} \max_{D} V(D,G) = E_{x\sim p_{data}(x)}[log(D(x))]+E_{z\sim p_z(z)}[log(1-D(G((z)))]

On va alors alterner entre :

      1. une montée de gradient pour D :

\max_{\theta_d} [E_{x\sim p_{data}(x)}log(D_{\theta_d}(x))+E_{z\sim p_z(z)}log(1-D_{\theta_d}(G_{\theta_g}((z)))]

      2. une descente de gradient pour G  :

\min_{\theta_g} [E_{z\sim p_z(z)}log(1-D_{\theta_d}(G_{\theta_g}((z)))]

afin de trouver l’optimum qui sera un point selle (ce qui implique des problèmes de résolution, explicités par la suite). Cette unique solution existe, où G découvre la distribution des données d’entraînement et D prédit une probabilité de 0.5 dans tous les cas.

Dans la publication d’origine G et D sont des perceptrons multicouches. Depuis, les réseaux à convolution, et parfois les réseaux récurrents sont majoritaires sur la plupart des cas d’usages. L’entraînement est fait par rétropropagation du gradient.

Formellement, on obtient l’algorithme suivant (source Goodfellow et al. 2014) : 

ainsi que les réseaux suivants pour l’exemple MNIST : 

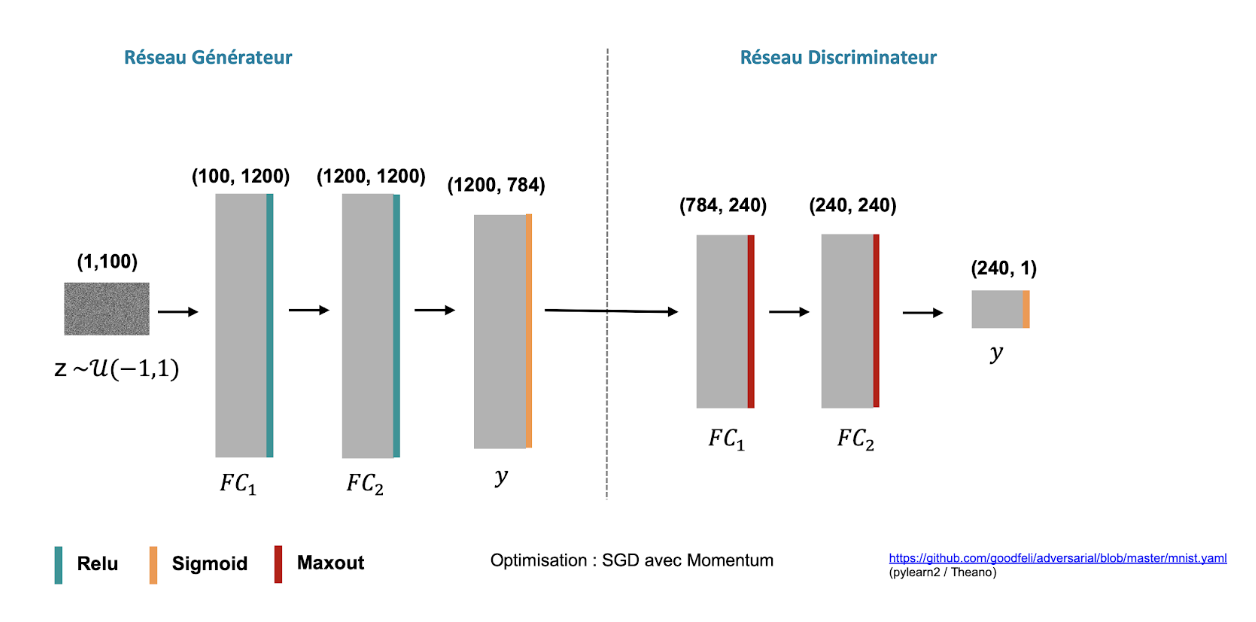
Les maths ne me font pas peur… est-ce que les vanilla GANs, ça marche ?

Les GANs présentent l’inconvénient d’être très délicats à entrainer voir ici pour un article expliquant les différentes difficultés et options d’implémentation en détail.

En effet, le problème d’optimisation initialement posé revient à trouver un point selle, ce qui peut poser problème. L’optimum des vanilla GANs revenant à trouver un équilibre de Nash entre deux joueurs non coopératifs, les updates de chacun ne garantissent donc pas la convergence globale.

Par ailleurs, de nombreux cas particuliers dans les données ne sont pas pris en compte dans le cadre théorique initial : que faire des valeurs manquantes, des variables catégorielles, des discontinuités ..?

Deux principaux problèmes calculatoires sont relevés dès la publication d’origine :

1. 1. « Vanishing gradient » : tôt dans l’apprentissage, lorsque G est par définition très faible, D va rejeter systématiquement les données synthétiques avec une forte confiance, auquel cas le gradient de G disparaît, on a alors un problème de saturation de log(1-D(G(z))) . Par conséquent, plutôt que minimiser log(1-D(G(z))) , on va plutôt entraîner G à maximiser log(D(G(z))) . Les dynamiques d’entraînement seront identiques, mais avec de plus forts gradients en début d’apprentissage.

Le problème d’optimisation est alors réécrit :

\max_{G}\max_{D} V(D,G) = E_{x\sim p_{data}(x)}[log(D(x))]+E_{z\sim p_z(z)}[log(D(G((z)))]

Ce problème de vanishing gradient peut ré-apparaître dès lors que G est suffisamment de qualité pour tromper D. Il peut alors devenir difficile de continuer son amélioration. C’est pourquoi, dans les extensions des GANs d’origine, on a tendance à se passer de cette probabilité de D, pour plutôt se baser sur une mesure de distance entre données synthétiques et réelles.

1. 2. « Mode collapse » : la propension de G à générer des exemples peu variés impliquée par le fait que plusieurs points du bruit aléatoire z sont associés à un point généré constant. Lorsque G génère un exemple synthétique qui dupe D avec un fort niveau de confiance, alors la caractérisation de cet exemple qui est un optimum pour G est indépendante du bruit z. Alors, G aura tendance à générer des points proches, et pourra passer à côté de schémas différents présents dans les données réelles. En pratique, un « mode collapse » partiel est commun. Cela s’explique par la structure même de la fonction objectif, basée sur les décisions de D et non pas sur l’adéquation entre la distribution des données générées et des données réelles. Plusieurs publications ont modifié le problème d’optimisation, pour se baser sur une couche intermédiaire du discriminateur, la « feature layer », plutôt que la sortie finale du discriminateur. Cela permettrait d’apprendre une meilleure représentation des données, et éviter le « mode collapse ».

De nombreuses bonnes pratiques en terme de création d’architecture de générateur et discriminateur ont été recensées au fil des publications pour pallier aux problématiques de l’entraînement des GANs. Dès Radford et Metz 2016 par exemple, le générateur d’un DCGAN se voit préconiser des activations ReLu sur chaque couche sauf la dernière, où on préconise tanh. Pour le discriminateur, plutôt LeakyReLu. Des recommandations sont également faites sur les types de couches, de strides etc.

Extensions : WGAN, DCGAN, bienvenue dans le “GANs zoo”

En 2017, Arjovsky et al. propose les Wasserstein GANs, qui deviennent par la suite très populaires et se distinguent de la façon suivante :

1. 1. Utilisation d‘une nouvelle fonction de perte basée sur la distance de Wasserstein-1 (ou Earth Mover, EM), plus de binary cross-entropy
   2. Weight clipping des poids de D au sein d‘un faible intervalle de valeurs (-c,c) afin d‘assurer d‘avoir une fonction objectif de G k-lipschitzienne. On lui assure ainsi d’éviter de détecter trop rapidement les données synthétiques et permet à G de continuer à s’améliorer. NB : cette façon de faire sera rapidement remplacée dans des publications ultérieures par un terme de régularisation du gradient, WGAN-GP
   3. Plutôt utiliser RMSprop qu‘Adam dont le momentum pourrait causer des instabilités dans l’entraînement

La sortie de D (dans le contexte WGAN appelé le Critic) est un scalaire indiquant le degré de réalisme de l’image générée plutôt qu’une probabilité d’appartenance. En effet, on retire la fonction d’activation sigmoïde.

De plus, à chaque itération, on met à jour le Critic avec plus d’itérations que G. Notons pour finir que les WGAN permettent de générer des données catégorielles et des améliorations sur la qualité des générations ont été proposées dans la célèbre publication de Gulrajani et al., 2017: « Improved Training of Wasserstein GANs ».

On obtient alors le schéma de fonctionnement suivant : 

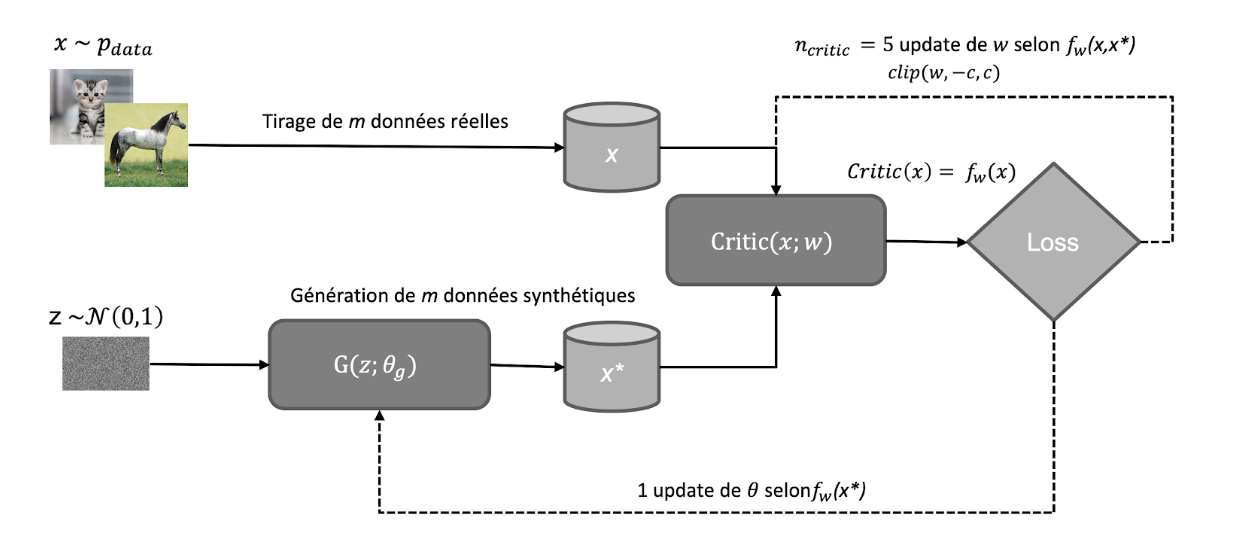
Il est à noter qu’en sus d’Earth-Mover, d’autres métriques de distance entre distributions ont été proposées en remplacement de Jensen-Shannon : Maximum Mean Discrepancy -MMD- (Sutherland et al. 2017, « Generative Models and Model Criticism via Optimized Maximum Mean Discrepancy », 42 citations)) et Cramér ou encore une distance d’énergie Bellemare et al., 2017 « The Cramer Distance as a Solution to Biased Wasserstein Gradients », 62 citations. La distance de Cramér a notamment été utilisée face aux biais que présentaient les WGAN entrainés par Stochastic Gradient Descent. En effet, il avait été illustré qu’ils pouvaient converger vers un minimum incorrect. La distance Cramér, qui a les mêmes propriétés souhaitables qu’Earth-Mover permet alors d’éviter ce biais.

Notons également que d’autres types de normalisations existent, notamment les Least Squares GANs (appliquent un moindres carrés entre la loss de D et sa sortie), Spectral Normalization GANs (contraignant avec une norme spectrale les points de chaque couche) et les Regularized GANs (ajout d’un bruit pour régulariser).

Pour étendre les applications, on peut également :

1. 1. 1. faire des conditional GANs, qui permettent de générer de façon conditionnée par des labels ou une information auxiliaire
      2. GANs bidirectionnels
      3. Adversarial Autoencoders
      4. Recurrent GANs pour les séries temporelles

Vous avez dit “buzz” ?

Les DCGAN (Deep Convolutional – GAN) sont très fréquents pour les cas d’usages image et utilisés largement dans les publications, ainsi que par le médiatisé collectif artistique NoArtist où le discriminateur est légèrement modifié afin de remplir une tâche de création artistique CAN (Creative Adversarial Networks) : Ils sont simplement des vanilla GANs avec une architecture convolutive, et entrainés grâce à l’astuce log(D(G(z))).

.

Nvidia (décembre 2018), pour la génération de visages ultra-réalistes, a utilisé une variante de DCGAN, en faisant grandir progressivement leur réseau : ProgressiveGAN. On note un entraînement sur 8 Tesla V100 GPUs pendant 4 jours, avec des batchs de 64 images de haute résolution.

Sur le site thispersondoesnotexist.com on peut trouver par exemple les images suivantes  : 

Plus récemment, le site generated.photos a fait le buzz en proposant une base de 100 000 visages générés, gratuitement téléchargeables sur leur Google Drive : 

Il est à noter qu’avec une résolution élevée, on peut quasiment systématiquement (pour l’instant) identifier les visages comme synthétiques. Cela se fait notamment par des incohérences au niveau des oreilles, ou encore un différentiel de flou entre le visage et l’arrière plan.

On parle également de plus en plus d’anonymisation de données, qu’elles soient tabulaires (cela fera l’objectif d’un article de blog dédié!) ou images voire vidéos.

On peut par exemple noter DeepPrivacy, solution d’anonymisation vidéo en cours de développement par des chercheurs de la Norwegian University of Science and Technology :

C’est éminemment plus complexe qu’anonymiser une photo dans la mesure où un GAN génère la nouvelle photo pour chaque frame, et doit respecter une cohérence temporelle, ce qui n’est pas encore le cas, bien que la vidéo soit effectivement anonymisée ! 

Après avoir vu Will Smith être Neo dans un Matrix nouvelle génération, on peut citer Hao Li, Associate professor à l’université de Southern California et l’un des pionniers du deepfake, qui affirme que d’ici six mois à un an, les deepfakes ne seront plus détectables par l’oeil humain..

Notons également, un challenge à la fin 2019 organisé notamment par Facebook et Microsoft, le DeepFake Detection Challenge, qui a pour vocation à permettre à la communauté de développer des algorithmes de détection de DeepFakes, notamment en prévision des élections de 2020. Ce challenge sera fortement sécurisé, afin que des hackers ne puissent justement pas récupérer les solutions identifiées.

Et pour finir, des bonnes nouvelles ! Appliqué à la recherche de nouveaux médicaments dans le secteur pharmaceutique, les GANs couplés à l’apprentissage par renforcement permettent de fortement diminuer les temps de recherche sur les premières phases de recherche de combinaisons de molécules. On note par exemple un premier vaccin anti-grippe développé en partie grâce à l’IA, et la plateforme MOSES (équipes In Silico Medecine notamment), disponible sur Github, qui propose un jeu de données open de molécules (ZINC), ainsi que plusieurs modèles déjà implémentés, notamment les Adversarial Autoencoders (combine des Variational Encoders avec un apprentissage de type GAN). 

A retenir

• Première publication en 2014, à elle seule >11.000 citations
• Les GANs sont une méthodologie élégante mais complexe pour générer de la donnée synthétique. Il y a de plusieurs difficultés d’entraînement à prendre en compte, mais les améliorations sont constantes en raison d’une recherche académique prolifique!
• Ils sont SOTA pour la génération d’image en particulier, mais les cas d’applications sont nombreux sur différents types de données
• Les DeepFakes, à l’heure actuelle basés sur des GANs (précédemment “juste” des swaps d’autoencodeurs) sont de plus en plus qualitatifs, et cela pose la question de la responsabilité des Data Scientists sur le sujet.
• Les GANs peuvent être un vrai game changer de l’IA, notamment en permettant de générer et partager de la donnée avec certaines propriétés beaucoup plus massivement. 
• Même si l’objectif est bien de générer de la donnée, il nous faut forcément de la donnée d’entraînement ! Sinon mieux vaut passer par des modèles théoriques.

Stay Tuned!

Un prochain article traitera d’un retour d’expérience de GANs appliqués à la génération de données tabulaires synthétiques, afin de remplacer des données réelles pour l’entraînement de modèles de Machine Learning type classification. Au programme : gestion des variables discrètes, catégorielles, mode collapse & co. 

✍Article écrit par Aurélia Nègre