Estimer l’incertitude de manière adaptative en régression avec MAPIE

L’incertitude des modèles de prédiction est une composante de la robustesse, propriété fondamentale d’un modèle d’IA qui consiste en la définition des limites de validité d’un modèle. Elle fait partie des 8 piliers de l’IA de confiance formalisés par Quantmetry et est décrite en détails dans cet article. Qu’est-ce que l’incertitude ? Pourquoi la rendre adaptative, selon quels critères ? Qu’est-ce que l’incertitude apporte à un modèle d’IA ? Ce sont les questions auxquelles nous répondrons, nous verrons aussi comment la mettre en place grâce à la bibliothèque MAPIE.

Incertitude

Qu’est-ce que l’incertitude ?

L’incertitude est une mesure de la confiance et donc de la fiabilité des prévisions. L’estimation de ces incertitudes est cruciale pour le développement de modèles d’IA fiables. Elle permet de mieux comprendre les prédictions de l’IA, de savoir quand le modèle est certain de sa prédiction et quand il l’est moins. Ceci permet de gérer les risques d’utilisation du modèle et finalement de prendre une décision éclairée : le modèle d’IA est davantage digne de confiance. Les nouvelles réglementations de l’AI Act rendront dans certains contextes et domaines sensibles cette estimation d’incertitude obligatoire (cf. Intelligence Artificielle de confiance – comprendre les enjeux de la prochaine décennie).

Comment la mettre en place ?

Il existe plusieurs manières de calculer ces incertitudes, nous choisissons de le présenter à travers les prédictions conformes, paradigme mathématique qui permet cette estimation de façon rigoureuse [1]. Nous ne parlons alors plus des classiques intervalles de confiance mais d’intervalles de prédiction qui nous apportent des garanties théoriques. Le modèle d’IA ne prédit plus uniquement une valeur mais un ensemble de valeurs; globalement nous sommes certains que dans x% des cas, la vraie valeur se trouve dans ces ensembles. La taille de cet ensemble nous fournit donc une mesure de l’incertitude grâce à laquelle nous pouvons interpréter la prédiction : plus il est grand, plus le modèle hésite entre différentes valeurs et donc moins il est certain de sa prédiction. A l’échelle d’une prédiction, c’est la taille de l’intervalle qui donne l’incertitude. A l’échelle du jeu de donnée, c’est la taille moyenne qui caractérise l’incertitude du modèle. La différence de tailles entre les intervalles, caractérise l’adaptabilité du modèle, c’est-à-dire sa capacité à distinguer les cas simples des cas compliqués.

En synthèse, une méthode de prédiction conforme se découpe en 3 étapes :

1. Entraînement : comme toute méthode de machine learning, il faut entraîner son modèle d’IA.
2. Conformalisation : la spécificité des prédictions conformes : choisir et calculer un score de conformité en fonction de son cas d’usage. Ce score transforme une heuristique d’incertitude en estimation rigoureuse de celle-ci.
3. Prédiction : calculer les intervalles (ou ensembles) de prédictions à l’aide de la sortie du modèle et des scores de conformité.

Prenons pour exemple deux modèles d’IA prédisant le prix d’une maison : le premier modèle donne un prix de la maison bleue à 1M€ avec un intervalle allant de 500 000€ à 1,4M€ et le second modèle prédit la même maison à 1,1M€ avec un intervalle de 900 000 à 1,3M€. C’est évidemment le deuxième modèle qui est plus certain de sa prédiction comme son intervalle est plus petit. Sans cette mesure d’incertitude, nous n’aurions pas su à quel modèle faire confiance.

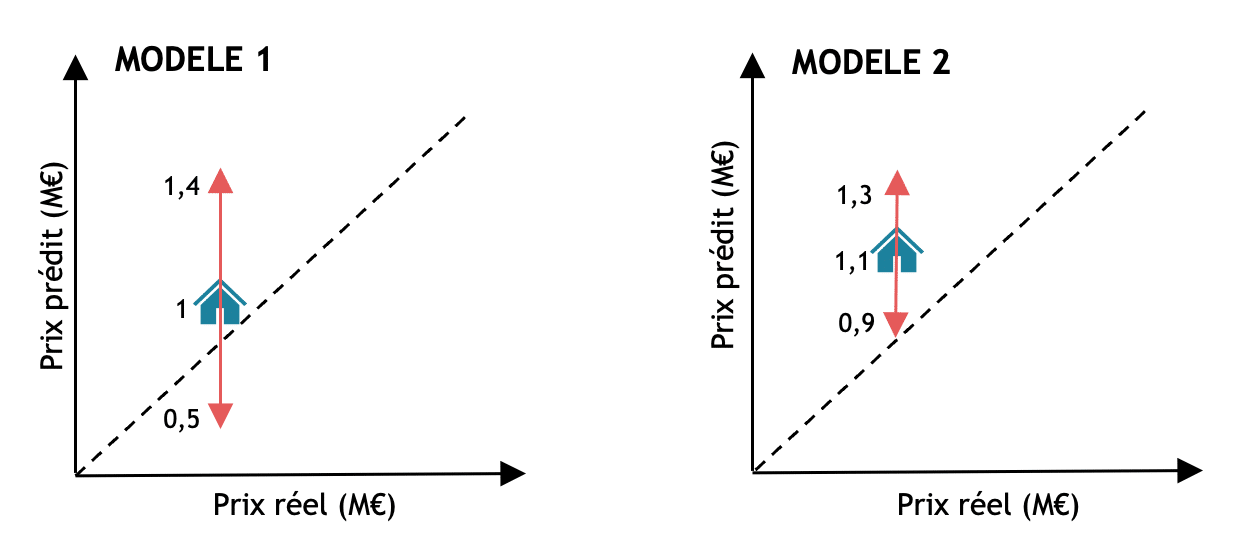
Figure 1 : Illustration schématique de deux modèles avec une estimation de l’incertitude grâce aux intervalles de prédictions (en rose). La ligne en pointillée représente un modèle parfait. Le modèle 2 est plus certain de la prédiction du prix de la maison puisque son intervalle est plus petit. Cependant pour la maison bleue, ce modèle 2 est plus éloigné de la réalité puisque moins proche de la ligne pointillée par rapport au modèle 1.

Incertitude adaptative

Qu’est-ce que l’incertitude adaptative ?

Alors que les méthodes originelles de prédictions conformes en régression donnaient des intervalles de taille constante pour toutes les données, nous avons aujourd’hui des techniques qui permettent d’estimer l’incertitude de manière adaptative. Nous appelons méthodes adaptatives les méthodes qui calculent des intervalles de tailles différentes pour chaque point des données. Cette adaptabilité permet d’appréhender la difficulté de chaque exemple individuellement : nous voulons un grand intervalle pour un point difficile à prédire et un petit sinon.

Si nous reprenons l’exemple précédent de prédiction du prix des maisons en ajoutant l’estimation d’incertitude adaptative. Les modèles 1 et 2 n’ont pas changés et prédisent toujours respectivement 1M€ et 1,1M€. Mais cette fois-ci l’intervalle autour de la prédiction du modèle 1 est plus petit (0.9M€ à 1,1M€) que celui du modèle 2 qui reste sensiblement le même. Que s’est-il passé ? Pourquoi l’intervalle de prédiction du modèle 1 est maintenant plus petit ? Et donc pourquoi avons-nous plus confiance en la prédiction de ce modèle 1 ? Dans le premier exemple, la conformalisation du modèle 1 a pu être perturbée par d’autres données sur lesquelles le modèle était moins certain, ce qui a causé au global des intervalles très grands. Alors que le modèle était certain de sa prédiction pour la maison bleue spécifiquement. Le modèle 2 est plus certain de ses prédictions globalement, mais sur la maison bleue en particulier, il l’est moins. L’adaptabilité ici nous a permis de comprendre plus finement notre modèle et de prendre une meilleure décision.

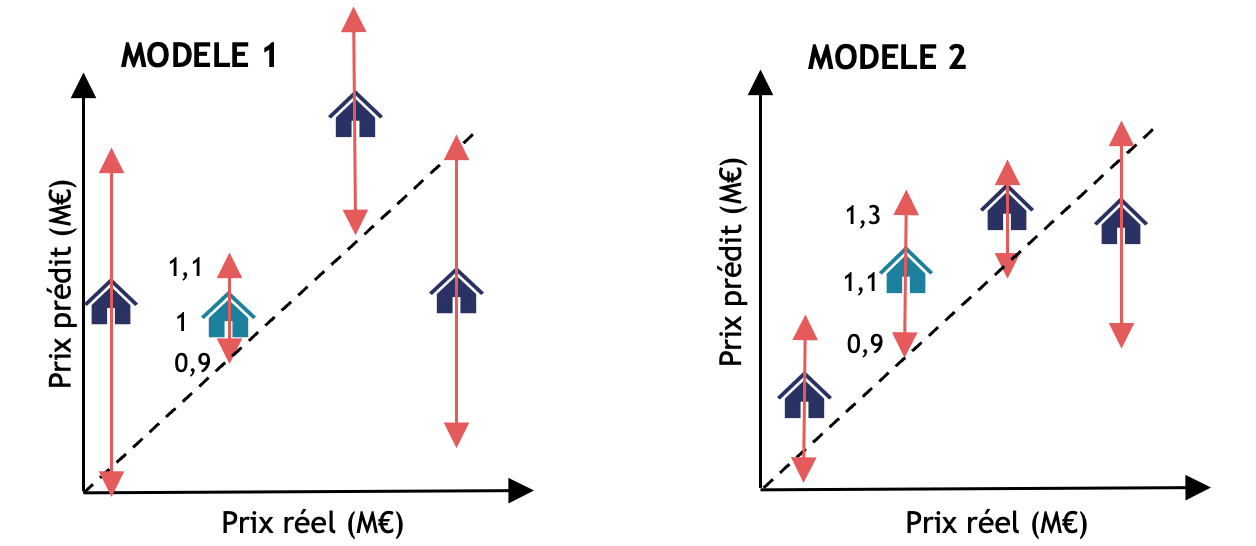
Figure 2 : Illustration des deux modèles précédents avec une estimation de l’incertitude adaptative. Les intervalles de prédictions sont représentés en rose. Les maisons violettes sont les autres données qui n’étaient pas représentées sur le schéma précédent mais qui avaient contribué au calcul des intervalles des méthodes non adaptatives de la figure 1. Grâce à l’adaptabilité, nous voyons finalement que c’était le modèle 1 qui était plus certain en sa prédiction sur la maison bleue.

Méthodes d’estimation d’incertitude adaptatives

En régression toujours, il existe deux grandes catégories de techniques pour estimer l’incertitude de manière adaptative. La première repose sur une technique spécifique : la méthode CQR (Conformalized Quantile Regression) [2] a été la première à traiter le cas d’incertitude adaptative en régression et est largement utilisée aujourd’hui. Malgré sa performance, nous ne pouvons pas l’utiliser avec n’importe quel modèle de régression puisqu’elle se base sur des régressions quantiles qui peuvent s’avérer très couteuses et inadaptées pour les modèles d’apprentissage profond.

Une autre technique pour obtenir des intervalles de tailles différentes est de définir un score de conformité adaptatif. C’est le cas par exemple du Gamma-score [3], qui donne des intervalles proportionnels à la prédiction, ou encore du Residual Normalised score [1] [4] qui prend en compte les variables d’entrée dans le calcul des intervalles et plus seulement les cibles. L’idée derrière ce dernier score est que des points anormaux véhiculent une plus grande incertitude.

Mesurer l’adaptabilité

En prédictions conformes, les métriques reconnues et les plus souvent utilisées sont des métriques globales. Nous parlons alors de couverture marginale : la part des points qui est bien dans l’intervalle de prédiction. Il existe néanmoins quelques métriques permettant de mesurer l’incertitude de manière locale [1][5]. En particulier, pour mesurer l’adaptabilité nous calculons une couverture pour chaque groupe de taille d’intervalles (autrement dit conditionnellement à la taille des intervalles).

MAPIE

Nous l’avons vu, les méthodes de prédictions conformes estiment l’incertitude en fournissant des garanties mathématiques sur la couverture globale [6]. Il existe de nombreuses techniques de prédictions conformes ce qui permet d’utiliser cette méthodologie sur des cas d’usages variés. Certaines d’entre-elles estiment l’incertitude de façon adaptative, nous apportant une compréhension encore plus fine du modèle.

Toutes ces méthodes peuvent être mise en place grâce à MAPIE [7] : solution open-source développée par Quantmetry dans le but de quantifier les incertitudes. Sont disponibles avec MAPIE des méthodes adaptatives mais aussi non-adaptatives pour la régression et la classification. Nous y avons récemment ajouté des métriques pour évaluer cette adaptabilité comme très peu sont disponibles aujourd’hui en prédictions conformes. MAPIE est compatible avec n’importe quel régresseur ou classifieur scikit-learn et est maintenu activement pour toujours proposer des méthodes à l’état de l’art !

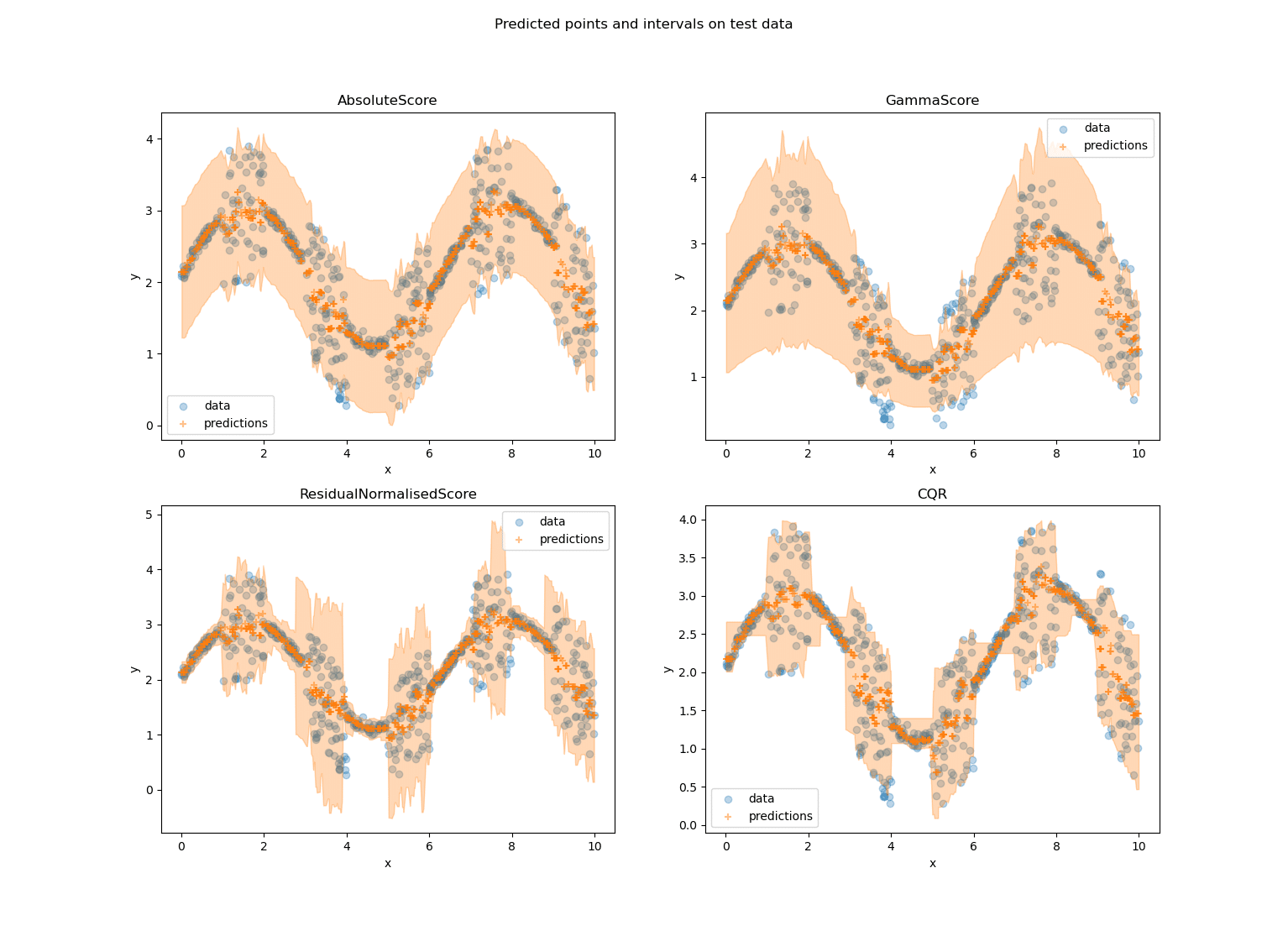
Figure 3 : Un exemple sur un jeu de données jouets des méthodes de régression de MAPIE. Les surfaces orange sur les graphes représentent les intervalles de prédictions. Nous observons clairement que la méthode Absolute score est une méthode non adaptative puisque ses intervalles sont quasi-constants. Gamma score est bien adaptative puisqu’elle donne des intervalles de tailles différentes mais n’est pas adaptée à ce jeu de données. En effet, cette méthode a la spécifité de donner des intervalles plus grands quand y est grand, il faut donc l’utiliser lorsque nous recherchons cette propriété : ce n’est pas le cas ici. Finalement, Residual Normalised score et CQR sont très satisfaisantes : les intervalles de prédictions collent bien aux données. Cependant, CQR est meilleure lorsque les données sont plus dispersées, tandis que Residual Normalised Score est meilleur pour les petits intervalles.

Ces graphes nous permettent de souligner un élément important : le choix de la méthode adaptative doit être fait en accord avec le cas d’usage. Prenons gamma score qui ici, malgré son adaptabilité, ne produit pas d’intervalles s’adaptant à l’incertitude des données. Cela arrive pour une raison simple : la spécificité de gamma score est qu’elle produit des intervalles plus grands quand y est grand. Cette propriété est intéressante et pertinente pour certains jeux de données et cas d’usage mais pas pour celui-ci spécifiquement. Quant à CQR et le score Residual Normalised, leurs intervalles s’adaptent bien à l’incertitude des données. Si nous avions affaire à un réel cas d’usage, le choix de la méthode se ferait alors en fonction de ce que l’on voudrait privilégier. En particulier ici, CQR est moins bon quand les données sont moins dispersées dans l’espace : les intervalles collent moins aux données, au contraire le score Residual Normalised est lui moins bon là où les données sont plus dispersées : il donne des intervalles plus grands que nécessaire.

Conclusion

Limitations et perspectives

Actuellement, la plus grande limitation de l’estimation de l’incertitude adaptative, est le manque de métrique. Les métriques d’adaptabilité mentionnées plus haut ne sont pas toujours simple à interpréter et ne transmettent pas toute l’information que nous voudrions, notamment concernant la sur-couverture (intervalle trop grand) et la sous-couverture (intervalle trop petit). C’est une perspective qui reste à explorer.

Ce qu’il faut retenir

Nous pouvons résumer les notions importantes de cet article en 4 points :

• Estimer l’incertitude de prédictions d’un modèle d’IA permet d’améliorer sa robustesse et finalement d’avoir un modèle plus digne de confiance.
• Les prédictions conformes permettent d’estimer l’incertitude avec des garanties mathématiques. Elles permettent de calculer des intervalles autour de chaque point de prédiction dont la taille est un indicateur de l’incertitude.
• L’incertitude adaptative c’est avoir des intervalles de tailles différentes : cas simple, petit intervalle et cas compliqué, grand intervalle.
• Il existe plusieurs méthodes pour estimer l’incertitude de manière adaptative (disponibles dans MAPIE), il faut choisir sa méthode en fonction de ses propriétés et des besoins du cas d’usage.

Références

[1] Angelopoulos, A. N., & Bates, S. (2021). A gentle introduction to conformal prediction and distribution-free uncertainty quantification. arXiv preprint arXiv:2107.07511.

[2] Romano, Y., Patterson, E., & Candes, E. (2019). Conformalized quantile regression. Advances in neural information processing systems, 32.

[3] Cordier, T., Blot, V., Lacombe, L., Morzadec, T., Capitaine, A., Brunel, N.. (2023). Flexible and Systematic Uncertainty Estimation with Conformal Prediction via the MAPIE library. Available from https://proceedings.mlr.press/v204/cordier23a.html.

[4] N. Seedat, A. Jeffares, F. Imrie, and M. van der Schaar, “Improving adaptive conformal prediction using self-supervised learning,” in International Conference on Artificial Intelligence and Statistics.

[5] S. Feldman, S. Bates, and Y. Romano, “Improving conditional coverage via orthogonal quantile regression,” Advances in neural information processing systems, vol. 34, pp. 2060–2071, 2021.

[6] V. Vovk, “Conditional validity of inductive conformal predictors,” in Asian conference on machine learning. PMLR, 2012, pp. 475–490.

[7] Taquet, V., Blot, V., Morzadec, T., Lacombe, L., & Brunel, N. (2022). MAPIE: an open-source library for distribution-free uncertainty quantification. arXiv preprint arXiv:2207.12274. PMLR, 2023, pp. 10 160–10 177.

Les membres de l’expertise Reliable AI développent des modèles performants, fiables et maîtrisés, sur l’ensemble du cycle de vie, pour une IA de confiance.

Candice Moyet

Data Scientist

Data Scientist chez Quantmetry, je travaille sur les sujets d’incertitudes et la bibliothèque MAPIE.