Les ordinateurs ont appris à bluffer. Et ça va tout changer ! (1/2)

Introduction

« Un grand maître d’échecs battu par un logiciel », « Victoire finale d’un algorithme contre les meilleurs joueurs de Go », « Une intelligence artificielle s’appuie sur sa mémoire pour maitriser différents jeux vidéo » …

Presque au quotidien, nous sommes submergés de nouvelles concernant des machines qui apprennent à jouer. D’ailleurs, chez Quantmetry, nous avons aussi contribué à cette tendance (1).

Cependant, les victoires récentes au poker du logiciel Libratus et de l’algorithme DeepStack changent véritablement la donne. Accompagnez nous dans ce voyage au coeur des comportements stratégiques et de l’intelligence (artificielle ou non) !

Théorie des jeux et asymétrie d’information

Principes de la théorie des jeux et dilemme du prisonnier

La théorie des jeux est définie comme “l’étude de modèles mathématiques de conflit et de coopération entre preneurs de décisions rationnels et intelligents”. Devenue un champ de recherche à part entière pendant les années 1940, avec la définition de l’équilibre de Nash dans les années 1950, la théorie des jeux a permis une meilleure compréhension de certains phénomènes jusque là peu étudiés: en particulier, les conditions qui permettent d’atteindre une coopérations entre plusieurs agents.

 John Nash dans les années 2000

L’exemple le plus connu d’une situation où une telle coopération n’est pas atteinte est le dilemme du prisonnier, énoncé par A. W. Tucker en 1950. Dans ce cadre, deux complices d’un crime sont retenus dans des cellules séparées et ne peuvent pas communiquer ; chacun d’entre eux peut décider de dénoncer l’autre ou de se taire.

Trois possibilités s’offrent à eux :

● si personne ne se dénonce, les deux prisonniers auront une peine minimale de 6 mois, faute d’éléments au dossier.

● si les deux se dénoncent entre eux, ils seront condamnés à une peine de 5 ans chacun.

● si un des deux prisonniers dénonce l’autre, il sera remis en liberté alors que le second obtiendra la peine maximale, soit 10 ans.

Cette situation peut être résumée ainsi :

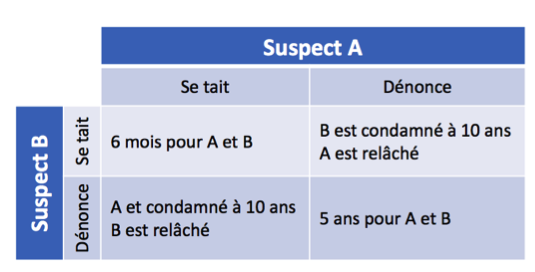
Il nous suffit de regarder ce schéma pour comprendre quelle serait la stratégie optimale pour les deux suspects s’ils étaient disposés à collaborer : se taire ! Si aucun des deux ne dénonce l’autre, leur peine cumulée sera la plus petite possible (un an). Cet état du système, dans lequel le bien-être d’un individu ne peut pas être amélioré sans détériorer celui d’un autre, est appelé optimum de Pareto. Notre intuition nous dit aussi que la solution à exclure est celle où les deux prisonniers dénoncent leur complice. Dans ce cas-là, ils auront une peine cumulée bien plus élevée (10 ans). Mais que va-t-il réellement se passer ?

Modéliser les interactions stratégiques grâce à la théorie des jeux

Une manière de résoudre ce problème est de se demander, pour chaque joueur, quelle serait sa meilleure stratégie en fonction de chaque stratégie de son complice.

Mettons nous à la place du suspect A. Comme nous ne savons pas ce que notre complice B décidera de faire, nous devons envisager les différentes possibilités :

● si nous faisons l’hypothèse que B va se taire, nous pouvons soit le dénoncer (et éviter la prison) soit nous taire (et recevoir une peine de 6 mois). En conclusion, sous cette hypothèse, nous avons intérêt à dénoncer notre complice.

● si nous faisons l’hypothèse que B va nous dénoncer, nous pouvons nous pouvons soit le dénoncer également (et recevoir une peine de 5 ans) soit nous taire (et recevoir une peine de 10 ans). En conclusion, sous cette hypothèse, nous avons également intérêt à dénoncer notre complice.

Dans tous les cas, notre meilleure stratégie est de le dénoncer ! Ce raisonnement est valable de manière symétrique pour le suspect B. Si les deux joueurs sont rationnels, chacun va dénoncer l’autre, ce qui amène à un résultat sous-optimal. La solution trouvée grâce à cette logique est l’équilibre de Nash du problème.

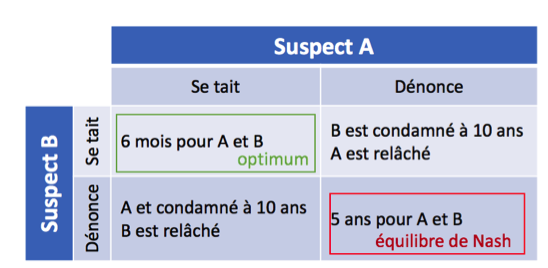
Enfin, ce cadre de pensée nous permet de comprendre pourquoi l’approbation et la mise en oeuvre d’un accord visant à réduire les émissions polluantes sera très complexe. Si les autres pays signent, on peut avoir dans le court terme un avantage concurrentiel en continuant à polluer comme avant ; et si les autres ne signent pas, on ne veut surtout pas être le seul à s’imposer des contraintes ! La recherche d’un compromis devra donc toujours partir de cette considération, pour ne pas risquer d’arriver à l’équilibre de Nash, très mauvais pour la planète…

Jeux répétés, asymétrie d’information et irrationalité des agents

Les situations étudiées par la théorie des jeux moderne sont bien plus complexes, et offrent des cadres théoriques à de nombreux problèmes de coopération, de concurrence, de différenciation entre produits etc. Nous allons présenter trois dimensions qui seront à retenir pour mieux comprendre Libratus et DeepStack.

Une interaction stratégique est d’habitude insérée dans un contexte plus riche, avec des interactions passées et futures : c’est le framework des jeux répétés. En particulier, si nous souhaitons répéter une interaction stratégique plusieurs fois, le choix optimal pourrait être d’avoir une “stratégie mixte”, i.e. de choisir nos options au hasard en maximisant une espérance de gain : un joueur de football aura tout intérêt à ne pas tirer tous ses penalties dans la même direction et de façon déterministe s’il souhaite continuer à marquer des buts !

Comme toute théorie mathématique, la théorie des jeux se base sur une hypothèse forte : la rationalité des agents, qui sont censés connaître et savoir quantifier les résultats de leurs actions dans n’importe quel contexte. Cependant, cette hypothèse est loin d’être vérifiée dans la réalité : évaluer l’effet de nos actions est parfois très compliqué, et même si nous arrivons à ce résultat c’est parfois un comportement irrationnel que nous choisissons d’adopter.

Deux chercheurs de l’université d’Hambourg ont mis des étudiants dans une situation similaire au dilemme du prisonnier, et ils ont trouvé que la collaboration entre eux a été beaucoup plus forte qu’attendu : les personnes n’ont pas toujours des comportement parfaitement rationnels, car de nombreux facteurs (surtout de nature sociale) affectent la prise de décision en plus de ceux analysés par la théorie des jeux.

Un autre aspect qui complexifie beaucoup le cadre théorique, mais qui permet de mieux décrire des cas réels, est l’asymétrie d’information. Au cours d’une négociation pour décider le prix d’un appartement, par exemple, le vendeur n’a pas intérêt à partager avec un possible acheteur le fait d’avoir besoin de vendre rapidement, ce qui pourrait faire baisser le prix. De la même manière, l’acheteur ne voudra pas communiquer à l’agent qu’il aura un enfant dans les prochains mois, et qu’il a donc besoin d’un appartement plus grand, coûte que coûte ! Si comme dans cet exemple chaque participant a un set d’informations spécifique qu’il n’a pas intérêt à partager, au moment de choisir notre stratégie nous devons faire des hypothèses sur les connaissances de notre adversaire.

Comment le Machine Learning tient-il compte de la théorie des jeux et de l’asymétrie d’information ?

Les systèmes de Deep Learning doivent gérer des situations avec information incomplète, comme c’était déjà le cas pour l’AlphaGo de DeepMind (Google). En parallèle, on observe une tendance lourde vers le développement d’ensembles d’algorithmes de Machine Learning, en compétition les uns avec les autres.

Par exemple, dans le cas des Generative Adversarial Networks (GANs), une méthode d’apprentissage non supervisée (Goodfellow et al. 2014), deux réseaux de neurones (un générateur et un discriminant) sont en concurrence pour générer de nouvelles images. Le générateur crée de nouvelles images, et le discriminant doit distinguer les vraies images parmi l’ensemble d’images fournies en entraînement, réelles ou synthétiques. D’un point de vue de la théorie des jeux, l’objectif du premier « joueur » (le discriminant) est d’apprendre à classifier correctement les images que lui sont proposées, alors que l’objectif du deuxième (le générateur) est d’arriver à tromper le discriminant, en générant des faux des plus en plus difficiles à identifier.

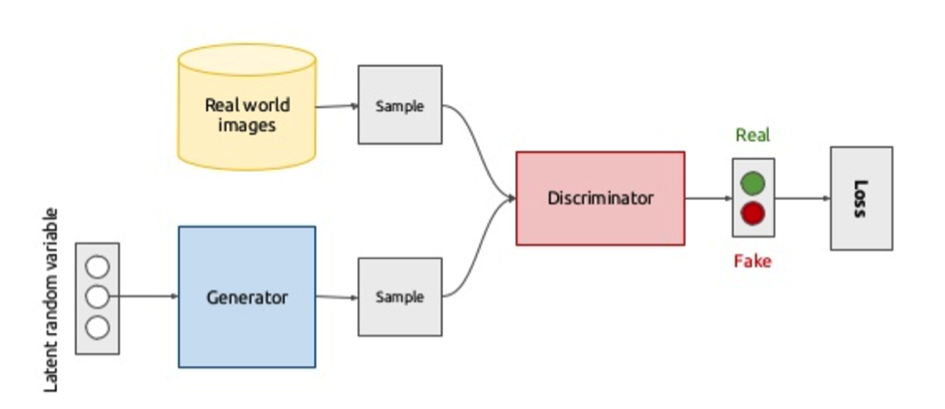
Cette structure est un jeu qui consiste à trouver un équilibre de Nash entre deux joueurs non coopératifs. Il est en effet possible de montrer qu’à l’équilibre les images créées par le générateur ne peuvent pas être identifiées par le discriminant, qui assigne à chaque image qu’il reçoit une probabilité de 50% d’être artificielle. On obtient ainsi une production d’images qui paraissent réaliste pour l’oeil humain. Cette technique a été récemment appliquée à des vidéos. Cependant, pour le moment, on n’arrive à produire des images et vidéos qu’avec un assez faible nombre de pixels.

Generated bedrooms. Source: “Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks” https://arxiv.org/abs/1511.06434v2

La théorie des jeux peut ainsi être une façon de construire une stratégie d’apprentissage, comme dans le cas des GANs, ou encore de prédire le comportement des autres individus participant à un jeu, comme dans le cas simpliste du dilemme du prisonnier et surtout dans toute situation réaliste impliquant plusieurs individus. Hartford et al (2016) utilise en effet le Deep Learning et la théorie des jeux pour prédire le comportement humain. En effet, la théorie des jeux comporte un large ensemble de modèles visant à prédire les décisions dans des contextes stratégiques, tout en incorporant des biais cognitifs et psychologiques. On est ainsi capable de généraliser et d’apprendre.

Un des objectifs classiques de l’AI est de réaliser un “robot” ou décideur qui soit perçu comme intelligent par un humain, i.e. qui passe le test de Turing. Or, les jeux permettent d’aller plus loin dans cette démarche en modélisant les interactions entre plusieurs agents, au lieu d’un seul.

Le robot peut donc interagir avec son environnement de façon bien plus naturelle : c’est grâce à ça qu’il pourra être beaucoup plus performant dans des cadres d’interactions complexes tels que le poker ou bien d’autres.

Dans un deuxième article, nous verrons les raisons qui font de Libratus une avancée majeure pour l’IA, ainsi que les cas d’application des approches combinées théorie des jeux/machine learning.

Références

– Radford, A., Metz, L., & Chintala, S. (2015). Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434.

– Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., … & Bengio, Y. (2014). Generative adversarial nets. In Advances in neural information processing systems (pp. 2672-2680), arXiv preprint arXiv:1406.2661

– Hartford, J. S., Wright, J. R., & Leyton-Brown, K. (2016). Deep learning for predicting human strategic behavior, Advances in Neural Information Processing Systems (pp. 2424-2432)

– Elpern-Waxman, J. (2017). Autonomous vehicles need to learn empathy and game theory

– Moravčík, M., Schmid, M., Burch, N., Lisý, V., Morrill, D., Bard, N., … & Bowling, M. (2017). DeepStack: Expert-level artificial intelligence in heads-up no-limit poker. Science, 356(6337), 508-513, arXiv preprint arXiv:1701.01724

– Zhao, J., Mathieu, M., & LeCun, Y. (2016). Energy-based generative adversarial network. arXiv preprint arXiv:1609.03126

– Garcia, V. (2016). La victoire d’un ordinateur sur un joueur de go n’est pas si revolutionnaire, L’express

– Gavois, S. (2016). Des échecs au jeu de Go : quand l’intelligence artificielle dépasse l’homme, NextInpact

– Moravčík, M., Schmid, M., Burch, N., Lisý, V., Morrill, D., Bard, N., … & Bowling, M. (2017). Deepstack: Expert-level artificial intelligence in no-limit poker. arXiv preprint arXiv:1701.01724.