Les prévisions probabilistes avec DeepAR

Prévoir le futur d’une série temporelle est un enjeu majeur dans de nombreux domaines: en météorologie, en finance pour prévoir l’évolution des cours boursiers, ou encore dans l’industrie pour prévoir la demande afin d’optimiser la supply chain et la planification. Contrairement aux prévisions ponctuelles qui visent à modéliser le comportement moyen du futur d’une série temporelle, les prévisions probabilistes ont pour but d’estimer une densité de probabilité ou une fonction quantile pour ces valeurs futures. Il n’est plus question de savoir que la consommation énergétique d’un logement donné sera de 60 kWh demain mais plutôt qu’il y a 95% de chance que cette consommation se trouve entre 58 et 61 kWh. Les intervalles de confiance deviennent les nouveaux objectifs des modèles car ils permettent d’estimer les valeurs extrêmes, souvent principale motivation d’une prise de décision. Récemment, de nouvelles méthodes de prédiction se sont développées afin de produire des modèles de prévision probabilistes. Parmi elles on trouve DeepAR, une méthodologie développée par Amazon AI dont le but est de produire des prévisions probabilistes grâce à un réseau de neurone autorégressif et récurrent entraîné sur une multitude de séries temporelles connexes. Ces avancées permettent de répondre à un besoin grandissant que l’on rencontre de plus en plus dans les problématiques business de nos clients.
Cet article a pour but de donner une brève introduction aux méthodes de prédiction probabilistes en se concentrant notamment sur la méthode DeepAR et son utilisation via le package Python GluonTS développé par Amazon Web Services.
A good forecaster is not smarter than everyone else.
He merely has his ignorance better organized.
Introduction
Qu’est-ce que la prévision ?
Combien de bouteilles d’eau Evian seront vendues cet été à Paris ? Combien d’iPhone seront vendus sur le site web de la Fnac le mois prochain ? La prévision est la science qui vise à décrire l’avenir. C’est un processus qui, basé sur des données historiques, cherche à établir l’évolution d’une grandeur à un horizon temporel donné. Il est important de noter la dépendance chronologique des séries temporelles : la valeur de la série à un instant donné n’est pas indépendante de son passé.
Différentes prévisions peuvent être produites à l’échelle d’une entreprise. Selon les exigences, plusieurs paramètres sont à déterminer :
- l’horizon temporel des prédictions : jour, semaine, mois, année, etc.
- la maille produit : modèle, article, gamme, quantités par magasin, etc.
- la maille géographique : continent, pays, région, etc.
Ces paramètres sont critiques car ils définissent directement les différents modèles qu’il peut être pertinent d’utiliser pour obtenir les prévisions les plus justes.
Les prévisions ponctuelles et les prévisions probabilistes
Il est important de noter que ce qui distingue la prévision des autres tâches d’apprentissage supervisé est le fait que les prévisions sont presque toujours fausses. En effet l’espace des prédictions dans un problème de classification ou de NLP est souvent fini alors que pour un problème de régression, comme la prévision de ventes, les possibilités offertes aux valeurs prises par les prédictions sont infinies. Dans ces conditions l’information obtenue par une mesure de prédiction ponctuelle est souvent partielle car relative au niveau de confiance de cette dernière. Cela revient en effet à se demander par exemple quelle est la probabilité de prédire exactement le nombre de chemises Adidas rouges taille M qui seront vendues la semaine prochaine ? Il est donc toujours nécessaire d’avoir non seulement une prévision ponctuelle, mais aussi une mesure de l’incertitude autour de cette prévision pour mieux décider.
L’incertitude de la prévision est aussi importante,
voire même plus importante, que la prévision elle-même.
Dans le cas des prévisions probabilistes, on ne s’intéresse plus tant à prévoir un comportement moyen de la série temporelle étudiée, mais plutôt à quantifier la probabilité d’un événement extrême. L’estimation de l’incertitude permet de créer des intervalles de confiance ou des fonctions quantiles, outils indispensables à la prise de décision. En effet, les décisions sont souvent fonction des extrêmes : il faut par exemple avoir assez de produits pour satisfaire la demande client, au risque d’en perdre pour cause d’épuisement des stocks ; ou encore ne pas avoir trop de produits périssables au risque de devoir les jeter. Les décisions sont également souvent asymétriques : en maintenance aéronautique, il est préférable d’avoir une vis en trop (coût ~ 50€) plutôt qu’une vis manquante (coût ~ 100K€ pour l’immobilisation d’un avion au sol). L’objectif est finalement d’avoir une estimation de la densité de probabilité des évènements futurs afin de pouvoir estimer, avec un certain degré de confiance, la bonne décision à prendre.
Modèle local et modèle global
Les modèles de prévision fréquemment utilisés aujourd’hui ont été développés dans le but de prédire le futur d’une série temporelle unique. Les méthodes de prévisions classiques, telles qu’ARIMA (modèle autorégressif à moyennes mobiles intégrées) ou ETS (lissage exponentiel), associent un modèle unique à chaque série temporelle, puis utilisent ce modèle pour prédire l’avenir de cette unique série temporelle. Par nature, ce type de modèle est appelé modèle local. Récemment, une nouvelle problématique a fait son apparition : il n’est plus seulement question de prédire le futur de séries temporelles individuellement, c’est plutôt le futur de milliers voire de millions de séries temporelles similaires qui doit être déterminé. Parmi les exemples, on trouve la consommation d’énergie par logement, la charge à répartir sur les serveurs d’un data center, ou encore la demande associée à chaque produit d’un site e-commerce. Pour ce type d’application, il peut être judicieux et bénéfique de construire un seul modèle commun à toutes ces séries temporelles connexes : par opposition à un modèle local, un tel modèle est dit global. Les paramètres du modèles sont ajustés grâce à l’ensemble des séries temporelles disponibles pour l’entraînement. Une fois le modèle établi, il permet ensuite de prédire le futur de toutes les séries temporelles semblables à celle vues pendant l’entraînement.
DeepAR : Autoregressive Recurrent Network
DeepAR est une méthodologie qui permet d’obtenir un modèle global de prévision basé sur un réseau de neurones autorégressif et récurrent. Le modèle est autorégressif car l’observation z du dernier pas de temps est utilisée comme entrée du réseau au pas de temps suivant et récurrent car la sortie du réseau h à un instant donné est réinjectée dans le réseau à l’instant suivant. (cf. notation Figure 2.)
Principe
Le but est d’estimer la distribution conditionnelle
![]()
qui représente le futur de chaque série temporelle 𝑧_(𝑖, 𝑡_0:𝑇) sachant son passé 𝑧_(𝑖, 1:𝑡_0-1) et les valeurs des variables exogènes pertinentes à tout instant 𝑥_(𝑖, 1:𝑇).
Apprentissage / Prédiction
Pour que l’apprentissage soit efficace, au moins 200 séries temporelles doivent être disponibles et elles doivent être générées par un même processus ou des processus similaires. En se basant sur ces données d’entrée, l’algorithme forme un modèle qui apprend une approximation de ces processus et l’utilise pour prédire la façon dont les séries temporelles évoluent. Tout d’abord, DeepAR forme le modèle en échantillonnant de façon aléatoire des exemples de formation sur chaque série temporelle. Chaque exemple de formation se compose de deux fenêtres adjacentes : une fenêtre de contexte et une fenêtre de prédiction. La taille de chacune de ces fenêtres est fixe et imposée par le paramètre context_length, qui permet de contrôler jusqu’où peut remonter le réseau dans le passé, et le paramètre prediction_length, qui permet de contrôler jusqu’où peuvent porter les prédictions dans le futur.
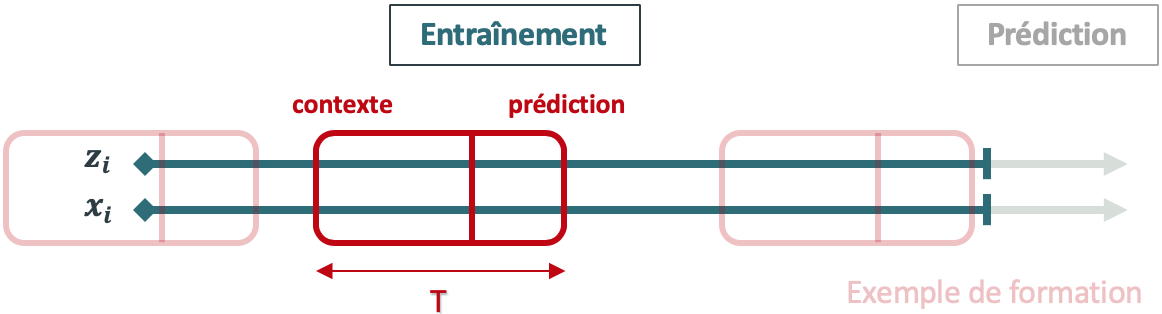
Figure 1. Mécanisme d’apprentissage de la méthode DeepAR
NB: la zone de prédiction de chaque exemple de formation doit se situer sur la plage d’entraînement, ce qui n’est pas nécessairement le cas pour la zone de contexte. Cela permet en particulier d’apprendre le comportement de cold-start, (i.e. réaliser des prédictions pour des grandeurs sans historique) lorsque la zone de contexte se situe avant t = 1.
Les paramètres du réseau sont ajustés en minimisant une fonction coût spécifique à chaque modèle (cf. détail des modèles ci-dessous). Les prédictions sont finalement des fonctions quantiles ou des intervalles de confiance obtenus grâce à l’agrégation d’exemples de prédictions ponctuelles.
Les variables exogènes
Chaque série temporelle est éventuellement associée à des variables exogènes statiques et/ou dynamiques qui peuvent être catégoriques (statut vacances, statut promotion, localisation magasin, etc.) ou à valeurs réelles (prix, nombre de clients, quantités vendues, etc.).
Un exemple de modèle paramétrique : AR2N2
Principe
Dans le modèle AutoRegressive Recurrent Neural Network (AR2N2) l’architecture du réseau de neurone récurrent (RNN) incorpore une loi de probabilité (gaussienne, binomiale négative, etc.) afin de produire la prévision probabiliste.
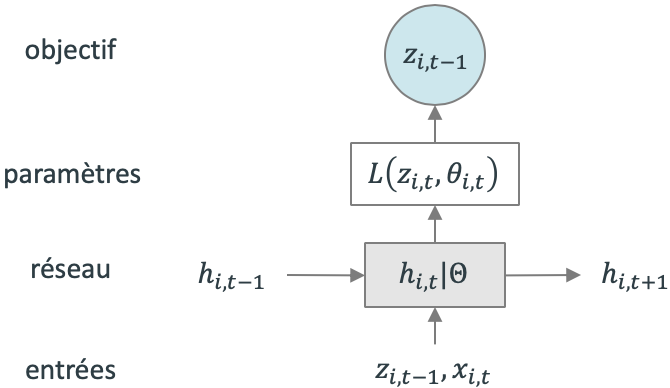 Figure 2. Architecture de AR2N2
Figure 2. Architecture de AR2N2
Le principe est simple : à chaque pas de temps, le but est de prédire la valeur au pas de temps suivant. Pour cela, le réseau reçoit en entrée la valeur de la série temporelle au dernier pas de temps 𝑧_(𝑖, 𝑡−1), les prédicteurs optionnels 𝑥_(𝑖, 𝑡) ainsi que sa propre valeur au pas de temps précédent ℎ_(𝑖, 𝑡−1). ℎ_(𝑖, 𝑡) représente la sortie du RNN au pas de temps 𝑡 et Θ représente l’ensemble des paramètres du RNN partagé ∀𝒊, 𝒕. Parmi ces paramètres se trouvent ceux qui définissent la distribution de probabilité, e.g. mu et sigma dans le cas d’une fonction gaussienne.
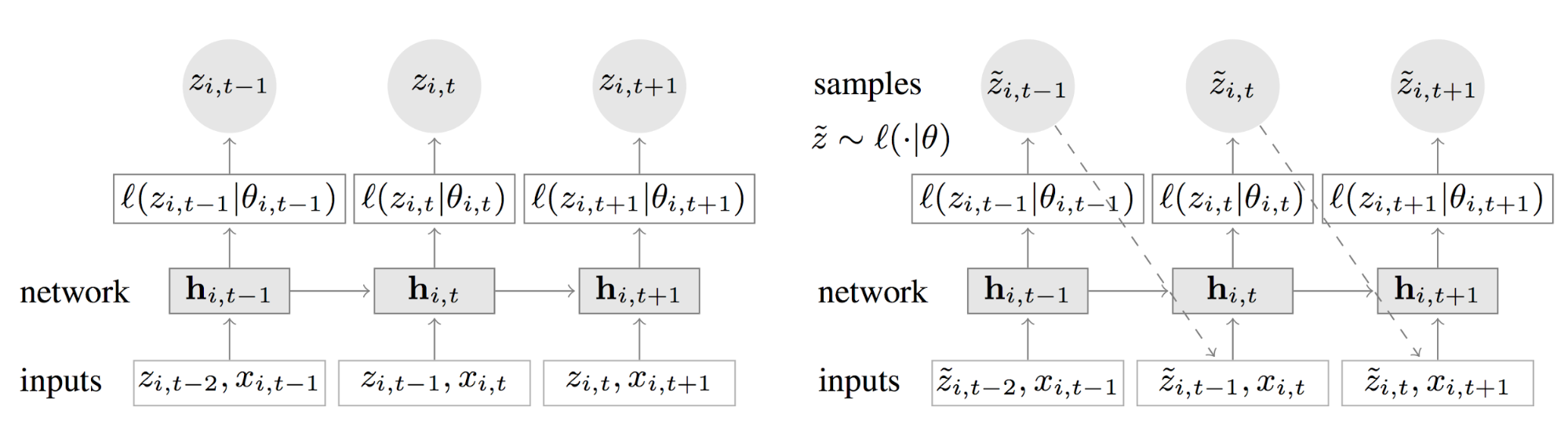
Figure 3. Illustration des mécanisme d’entraînement (à gauche)
et de prédiction (à droite) du modèle AR2N2
Entraînement
Pendant l’entraînement, on cherche à ajuster les paramètres Θ jusqu’à obtenir convergence. Ces paramètres Θ correspondent à la fois aux poids internes du réseau et aux poids qui définissent le mapping entre la sortie du réseau et les paramètres de la distribution. Pour ajuster ces poids, on fait passer chaque exemple de formation par notre réseau, ce qui nous permet d’obtenir les paramètres de la loi de distribution. Ensuite, on calcule la fonction de log-vraisemblance associée à notre modèle de probabilité qu’on minimise par descente de gradient afin de mettre à jour l’ensemble des poids du réseau.
Prédiction
Une fois le modèle entraîné, il est alors possible de réaliser une prédiction. Dans un premier temps, on prédit la loi de probabilité à l’instant suivant. Ensuite, on réalise le tirage d’une valeur de cette distribution qui représente une prédiction ponctuelle. Cette valeur devient l’entrée du réseau au pas de temps suivant, et ainsi de suite jusqu’à l’horizon de prédiction. Chaque fois qu’on réitère ce processus, on génère une nouvelle exemple de prédiction entre t_0 et T. L’ensemble des exemples de prédiction permet ensuite d’obtenir des fonctions quantiles ou d’estimer des intervalles de confiance.
Modèle de vraisemblance
Le modèle de vraisemblance choisi modélise le “bruit” et doit correspondre aux propriétés statistiques des données. Le choix de la loi de probabilité (gaussienne, binomiale négative, t-Student, poisson, etc.) est donc une étape cruciale dans l’établissement de ce modèle. Par exemple, on peut paramétrer une fonction gaussienne avec sa moyenne et sa variance, où la moyenne est une transformation affine de la sortie du réseau et la variance une fonction affine de la sortie du réseau suivi d’une fonction d’activation softplus afin de garantir sa positivité. Le modèle de vraisemblance est alors le suivant :
![]()
Commentaires
Ce modèle nécessite des hypothèses fortes sur les données. En effet, on postule sur une loi de distribution donnée pour les valeurs futures de la série temporelle. De plus, la modélisation de lois de distribution plus complexe est difficile car il faut pouvoir obtenir une fonction de vraisemblance et que celle-ci soit facilement calculable et implémentable. Cependant, ce modèle présente l’avantage d’avoir un faible nombre de paramètres à estimer.
Un exemple de modèle non paramétrique : SQF-RNN
Principe
Dans le modèle Spline Quantile Function with Recurrent Neural Network (SQF-RNN) l’architecture est similaire à celle du modèle AR2N2. Cependant l’objectif n’est plus de trouver les paramètres d’une loi de distribution fixée mais de modéliser directement les fonctions quantiles par une régression par spline linéaire isotone.
Pour rappel, une régression isotone est une technique de modélisation d’un nuage de points par une forme libre qui doit être monotone et « aussi proche que possible des données » (souvent d’un point de vue des moindres carrés). Une spline par ailleurs est une fonction définie par morceaux par des polynômes. La figure 4. illustre la modélisation d’une fonction quantile par une spline linéaire isotone.
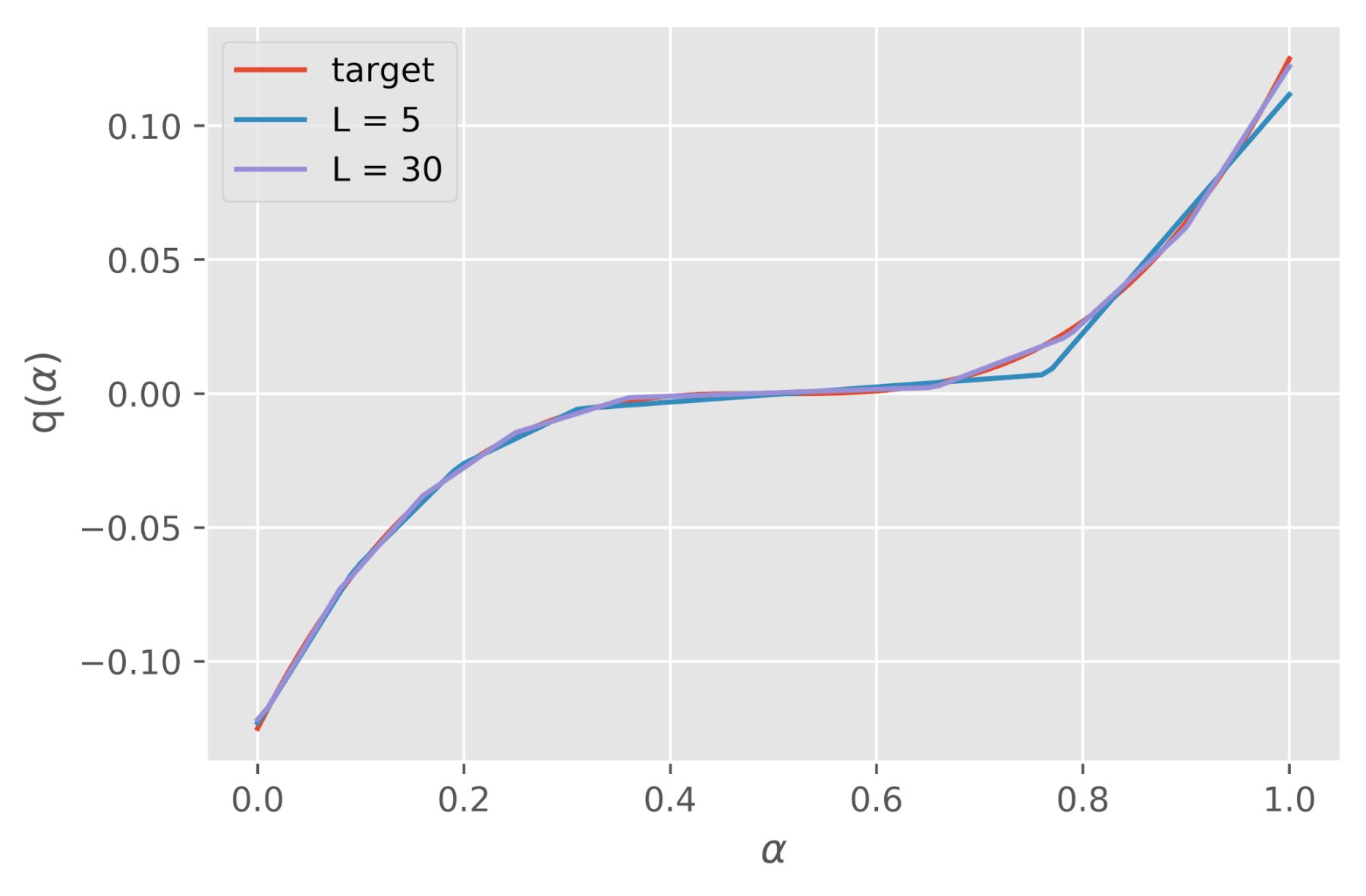
Figure 4. Modélisation d’une fonction quantile par une spline linéaire isotone
avec différents nombres de noeuds
Les splines linéaires isotones sont définies par :
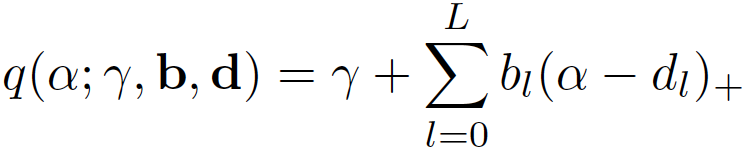
où gamma correspond à l’ordonnée à l’origine, L au nombre de noeuds, b aux pentes des fonctions par morceaux, d aux positions des noeuds et la fonction (x)+ représente la fonction ReLU = max(0, x).
Les paramètres de notre modèle sont donc l’ensemble des poids du réseau de neurones ainsi que tous les coefficients qui réalisent le mapping entre la sortie du réseau de neurones et les paramètres gamma, b et d qui caractérisent les splines. La fonction de coût utilisée pour optimiser ces paramètres est la fonction “Continuous Ranked Probability Score” (CRPS). Cette fonction est une généralisation de la pinball loss utilisée pour estimer une fonction quantile donnée. Cette fonction présente en particulier la propriété d’être une “proper scoring rule” (fonction score exacte) qui signifie que si les données sont générées par une distribution G, alors le CRPS est minimisé si la distribution prédite F est égale à G.
L’architecture du modèle est définie comme suit :
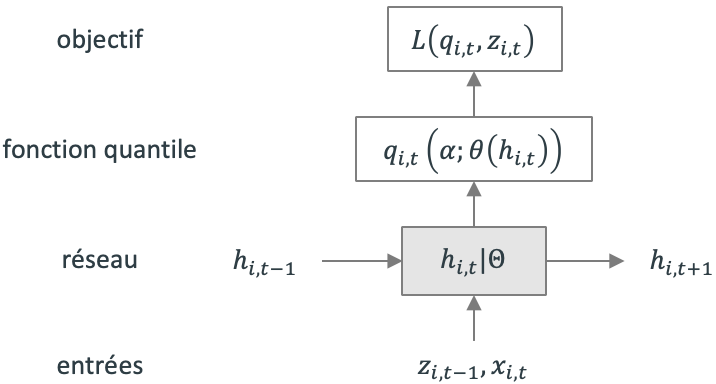 Figure 5. Architecture du modèle SQF-RNN
Figure 5. Architecture du modèle SQF-RNN
En entrée, le réseau le réseau reçoit la valeur de la série temporelle au dernier pas de temps 𝑧_(𝑖, 𝑡−1), les prédicteurs optionnels 𝑥_(𝑖, 𝑡) ainsi que sa propre valeur au pas de temps précédent ℎ_(𝑖, 𝑡−1). ℎ_(𝑖, 𝑡) représente la sortie du RNN au pas de temps 𝑡 et Θ représente l’ensemble des paramètres du RNN partagé ∀𝒊, 𝒕. Parmi ces paramètres se trouvent ceux qui définissent les paramètres des fonctions quantiles (gamma, b et d).
Entraînement
Pendant l’entraînement, on cherche à ajuster les paramètres Θ jusqu’à obtenir convergence. Ces paramètres Θ correspondent à la fois aux poids internes du réseau et aux poids qui définissent le mapping entre la sortie du réseau et les paramètres des fonctions quantiles. Pour ajuster ces poids, on fait passer chaque exemple de formation par notre réseau, ce qui nous permet d’évaluer la fonction CRPS qui est ensuite minimisée par descente de gradient.
Prédictions
Sur la plage de prédiction, un échantillon \hat{z}_(i, t)=q_{θ(h_(i, t))}(α) avec α suivant une loi uniforme U(0, 1) est tiré et injecté comme entrée au réseau pour le pas de temps suivant, jusqu’à l’horizon de prédiction. La répétition de cette démarche produit un ensemble d’échantillons de prédictions sur la plage de prédictions qui permet d’évaluer ensuite tout intervalle de confiance ou même une fonction quantile précise.
Commentaires
Contrairement au modèle AR2N2, le modèle SQF-RNN ne nécessite aucune hypothèse sur les données. Par nature, le modèle SQF-RNN est capable de modéliser des distributions complexes grâce à l’utilisation des splines. Le nombre de paramètres est cependant plus important que pour le modèle AR2N2 mais l’utilisation du réseau de neurones permet d’estimer tous ces paramètres relativement facilement.
Un peu de code avec GluonTS
GluonTS est une boîte à outils construites sur Apache MXNet qui permet de créer des modèles probabilistes pour les séries temporelles. GluonTS permet en particulier d’implémenter les différents types de modèles DeepAR que nous avons vu précédemment :
AR2N2 d’une part, où l’objectif est de déterminer les paramètres d’une distribution fixée (loi gaussienne comme vu dans cet article, ou autre)
SQF-RNN d’autre part, où l’objectif est de déterminer directement les paramètres des fonctions quantiles
Quel que soit le type de méthode, le framework proposé reste identique à la seule différence de la fonction qui fait correspondre la sortie du réseau de neurone aux paramètres qui permettent de déterminer la distribution.
Préparation des données
Afin d’être compatibles avec GluonTS, les données doivent être mises à un format particulier. Des fonctions internes à GluonTS permettent de le faire très facilement. Sous forme de dictionnaire, il suffit de définir:
la série temporelle sous forme de liste (ex. [1, 0, 3, 2, 3, 1])
la date de début de la série temporelle sous forme de timestamp (ex.)
la fréquence de la série temporelle (jour ‘D’, heure ‘H’, etc.)
optionnellement, des variables exogènes catégoriques et/ou numériques, statiques et/ou dynamiques sous forme de listes.

NB: Dans l’exemple ci-dessus, context_length = 6 et prediction_length = 2. Il est important de noter que les variables exogènes dynamiques doivent toujours faire la même taille que la série temporelle complète (donc ici 8). Il peut également y avoir plusieurs variables dans chaque catégorie.
Entraînement
Les modèles prédéfinis dans GluonTS prennent en entrée une fenêtre de longueur context_length et prédisent la distribution des valeurs de la fenêtre suivante de longueur prediction_length. Dans GluonTS, on appelle Estimator un objet qui représente un modèle de prévision ainsi que l’ensemble des paramètres qui permettent de le définir (coefficients, poids, etc.). En général, chaque Estimator est paramétré par un certain nombre d’hyperparamètres qui peuvent être commun à tous les modèles (e.g. prediction_length) ou spécifiques à un estimateur particulier (nombre de couches pour le réseau de neurones, etc.) Enfin, chaque estimateur est configuré par un Trainer qui définit comment est entraîné le modèle: nombre d’epochs, learning rate, taille des batchs, etc. Le modèle prend aussi comme argument une distribution qui nous permet d’évaluer nos observations et de laquelle on tire nos prédictions. En pratique, déclarer cette distribution permet de configurer la couche de projection qui se situe à la sortie du RNN et lie les coefficient en sortie de ce RNN aux paramètres de notre distribution (𝜇 et 𝜎 pour une distribution gaussienne du modèle AR2N2, ou gamma, b et d pour les spline du modèle SQF-RNN).

Après avoir spécifié notre estimateur avec tous les hyperparamètres nécessaires, nous pouvons entraîner notre modèle en invoquant la méthode train de notre Estimator. L’algorithme d’entraînement renvoie un modèle entraîné ou, dans le langage GluonTS, un Predictor qui va nous permettre de construire nos prédictions.
![]()
Prédictions
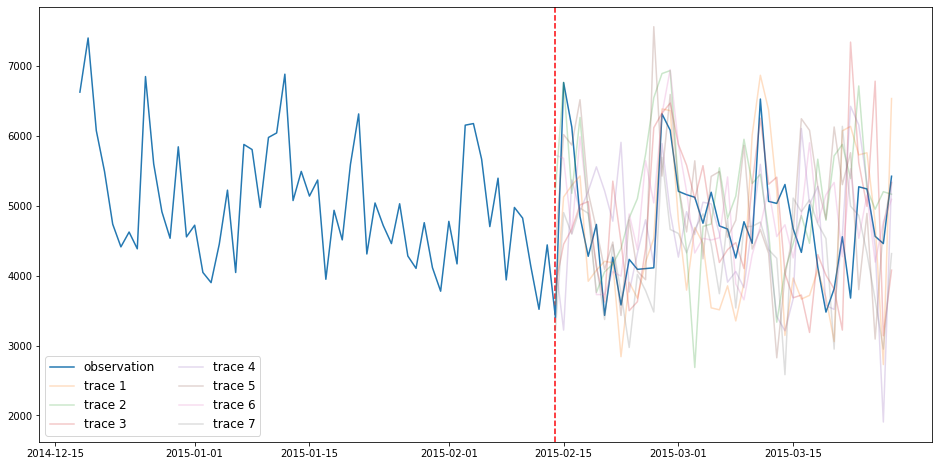
GluonTS propose une fonction `make_evaluation_predictions` qui automatise le processus de prédiction et d’évaluation du modèle. De manière synthétique, cette fonction réalise les tâches suivantes:
- Enlever la dernière fenêtre de `test_ds` de longueur `prediction_length` que nous voulons prédire.
- L’estimateur utilise toutes les données disponibles pour prédire (sous la forme de _sample paths_) la fenêtre future que nous venons d’ôter.
- La sortie du module sont les _sample paths_ prédits (sous forme de générateur d’objet python)

GluonTS possède également des fonctions qui permettent de visualiser les prévisions réalisées et d’estimer les performances du modèle :
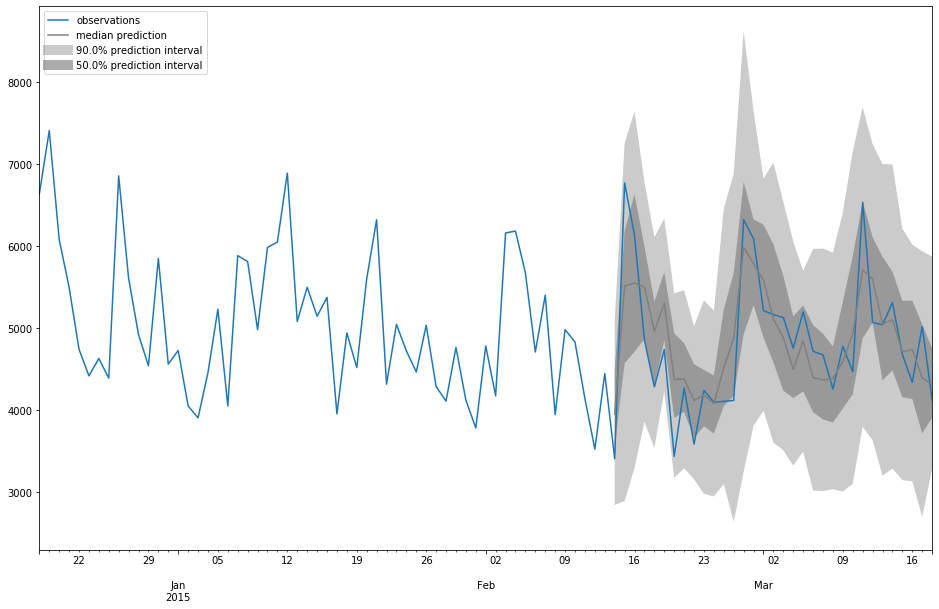
Evaluation
De nombreuses métriques sont directement définies dans l’objet Evaluator:


Conclusion
L’analyse de séries temporelles et les prévisions n’ont toujours pas atteint leur âge d’or et restent aujourd’hui un domaine dominé par les modèles statistiques. Les derniers résultats de la compétition de forecasting M4 montrent que deux mondes sont en train de s’accoster pour créer des approches hybrides entre modèles statistiques et modèles de machine/deep learning. Il est à noter que, dans le cas de la construction de modèles globaux lorsqu’une centaine de séries temporelles connexes sont à disposition, DeepAR permet de créer des modèles très performants, autant pour des prévisions ponctuelles que pour des prévisions probabilistes.
✍Article écrit par Vincent Fighiera
Références
Makridakis, S., Hogarth, R.M. & Gaba, A. (2009) Forecasting and uncertainty in the economic and business world. International Journal of Forecasting.
Salinas, D., Flunkert, V., & Gasthaus, J. (2017). DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks. Retrieved from http://arxiv.org/abs/1704.04110
Gasthaus, J., Benidis, K., Wang, Y., Rangapuram, S. S., Salinas, D., Flunkert, V., & Januschowski, T. (2019). Probabilistic Forecasting with Spline Quantile Function RNNs. Proceedings of Machine Learning Research, 89, 1901–1910.
Alexandrov, A., Benidis, K., Bohlke-Schneider, M., Flunkert, V., Gasthaus, J., Januschowski, T., … Wang, Y. (2019). GluonTS: Probabilistic Time Series Models in Python. 1–24. Retrieved from http://arxiv.org/abs/1906.05264

