Les valeurs de Shapley en intelligibilité locale des modèles

De plus en plus utilisés par les entreprises, les algorithmes de Machine Learning sont parfois tellement complexes qu’ils se révèlent être de véritables boîtes noires (réseaux de neurones, SVM, forêts aléatoires…). Ces modèles perdent en explicabilité ce qu’ils gagnent en précision.
Dans certains cas, les applications de ces modèles boîtes noires sont particulièrement sensibles : diagnostics médicaux, octroi de crédit… Pour cette raison, l’Union Européenne a mis en place certaines dispositions dans son RGPD (Règlement Général pour la protection des données) afin d’obliger les entreprises à expliquer simplement les prévisions des algorithmes d’apprentissage automatique qu’elles utilisent.
Se pose également la question du transfert de connaissances de la machine vers l’homme, pour que l’intelligence artificielle serve également à une plus grande compréhension du domaine d’application.
Pour répondre à ces enjeux, un nouveau champ de recherche se développe depuis plusieurs années : l’intelligibilité des modèles de Machine Learning, que ce soit pour des données tabulaires, du texte ou des images. Nous y avons consacré notre livre blanc « IA explique toi ! ».
Dans cet article, nous nous penchons plus particulièrement sur une méthode d’intelligibilité : les valeurs de Shapley et leur estimation avec la bibliothèque Python SHAP.
A quel niveau intervient l’intelligibilité ?
L’intelligibilité vient après l’étape de modélisation (celle où l’on construit le modèle prédictif). Cette phase ne fait plus appel à des algorithmes prédictifs entrainés mais à des algorithmes d’intelligibilité, pour expliquer les prédictions du modèle prédictif précédemment construit.
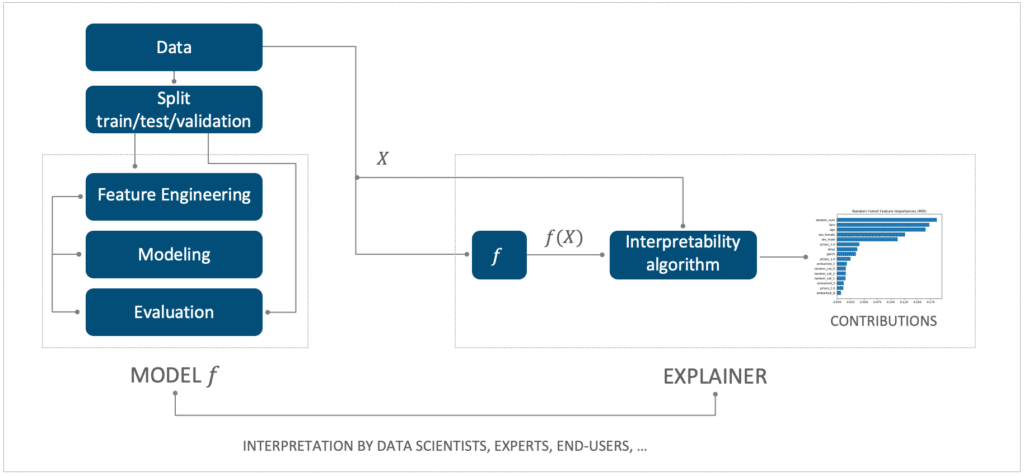
Figure 1. L’intelligibilité est une étape dissociée de la modélisation
L’objectif général de l’intelligibilité est de mieux comprendre les modèles ou leurs prévisions. Cela consiste à pouvoir expliquer simplement les prévisions d’un modèle.
On distingue deux types d’intelligibilité : l’intelligibilité locale et l’intelligibilité globale.
- L’intelligibilité globale cherche à expliquer le modèle dans sa globalité. C’est-à-dire quelles sont les variables les plus importantes en moyenne pour le modèle.
- A contrario, l’intelligibilité locale, consiste à expliquer la prévision f(x) d’un modèle pour un individu x donné.
Dans cet article nous nous intéresserons particulièrement à l’intelligibilité locale.
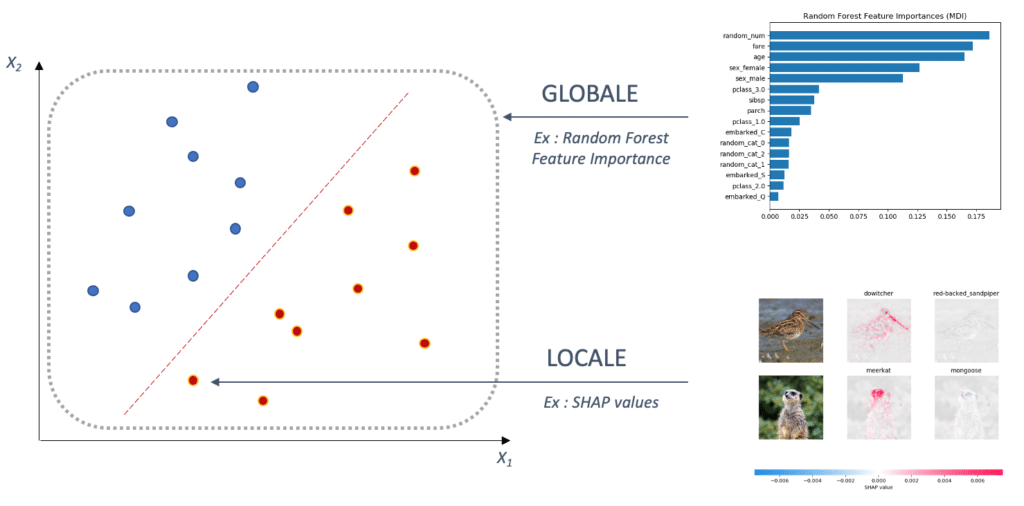
Figure 2. L’intelligibilité locale explique la prédiction d’un point, tandis que l’intelligibilité globale explique le modèle dans ses grandes tendances.
Une méthode d’intelligibilité locale : les valeurs de Shapley en Machine Learning
Il existe de nombreux algorithmes d’intelligibilité, souvent empiriques sans beaucoup de justifications théoriques. C’est là l’une des raisons principales pour lesquelles la bibliothèque Python SHAP a été créée en 2017 par Scott Lundberg à la suite de sa publication [1], pour proposer des algorithmes d’estimation des valeurs de Shapley, une méthode d’intelligibilité reposant sur la théorie des jeux coopératifs.
Depuis son lancement, cette bibliothèque connaît un succès grandissant, notamment grâce à de meilleures justifications théoriques et des visualisations qualitatives.
Nous présentons ci-dessous le principe général de ces valeurs de Shapley en intelligibilité.
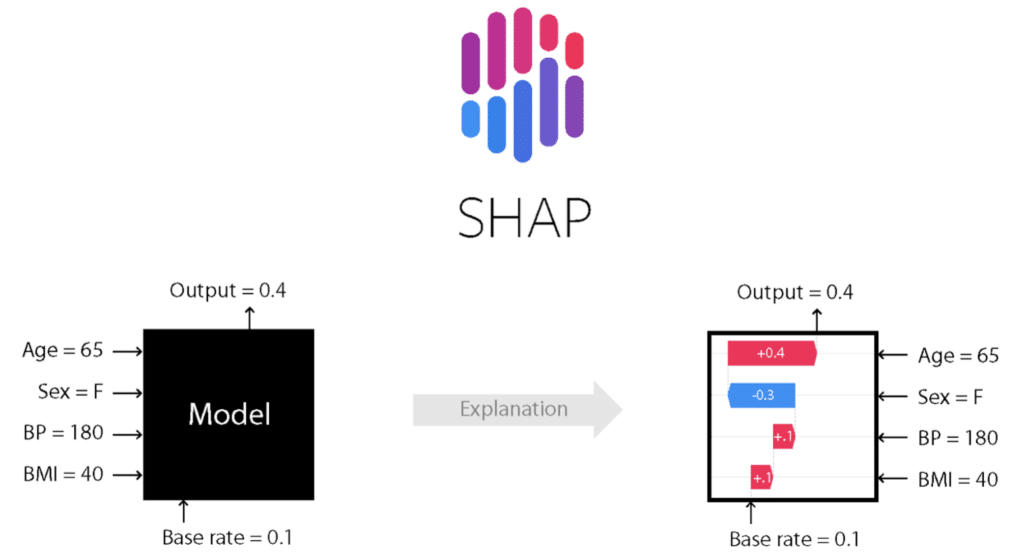
Figure 3. SHAP permet de traduire la prédiction d’un individu en explication sous forme de somme de contributions de chacune des variables. Schéma issu du projet Github SHAP
Voici un exemple de scénario illustré sur le schéma ci-dessus : un hôpital utilise un modèle prédictif pour calculer une probabilité de décès des patients en fonction de caractéristiques physiques. Sont pris en compte, l’âge, le sexe, la pression sanguine (BP pour “Blood Pressure”) et l’indice de masse corporelle (BMI pour “Body Mass Index”, IMC en français). On suppose que l’algorithme est un modèle boîte noire.
Le Data Scientist à l’origine de ce modèle souhaite expliquer le résultat obtenu pour une patiente de 65 ans, qui a un IMC de 40 et une pression sanguine à 180. L’algorithme a prédit une probabilité de décès de 0.4.
Expliquer la prédiction à l’aide des valeurs de Shapley consiste à attribuer à chaque variable d’entrée, plus précisément à chaque valeur décrivant l’individu considéré (“65 ans”, “Femme”, “180” de pression sanguine et “40” d’IMC) un coefficient réel. Chacun de ces coefficients indique comment cette valorisation a contribué à décaler la prévision à 0.4 de la moyenne globale de 0.1 des prédictions. La somme des contributions de Shapley est égale à cet écart :
(1) ![]()
Sur cet exemple, les valeurs de Shapley nous indiquent que l’individu est à risque en premier lieu à cause de son âge, et dans une moindre mesure à cause de sa pression sanguine et de son IMC qui sont tous deux élevés.
A contrario, le sexe du patient fait baisser ce risque de décès, sans toutefois le compenser totalement. Les valeurs de Shapley permettent de retrouver l’intelligibilité de modèles plus simples comme les régressions linéaires.
Pour déterminer ces coefficients, les valeurs de Shapley définies en Machine Learning font appel à la théorie des jeux coopératifs.
Les valeurs de Shapley ou comment répartir équitablement un gain entre plusieurs joueurs dans un jeu coopératif ?
En théorie des jeux coopératifs, le cadre est le suivant : n joueurs collaborent ensemble et obtiennent un gain G. La question est : comment répartir de manière équitable le gain entre les n joueurs ?
« Équitable » signifie ici « en prenant en compte la contribution des joueurs dans l’obtention du gain ». Cela veut dire que l’on ne rémunère pas un joueur uniquement pour ce qu’il est capable d’obtenir comme gain lorsqu’il est seul, mais également pour sa contribution au groupe, lorsqu’il interagit avec les autres joueurs.
Pour répondre à cette question, on suppose disposer du nombre de joueurs ![]() , d’une fonction
, d’une fonction ![]() (où
(où ![]() ) caractéristique du jeu, indiquant pour chaque coalition de joueur (sous-ensemble de joueurs) le gain maximal qu’ils peuvent obtenir en collaborant.
) caractéristique du jeu, indiquant pour chaque coalition de joueur (sous-ensemble de joueurs) le gain maximal qu’ils peuvent obtenir en collaborant.
Le gain total ![]() est le gain
est le gain ![]() qu’obtiennent tous les joueurs lorsqu’ils collaborent ensemble.
qu’obtiennent tous les joueurs lorsqu’ils collaborent ensemble.
Théorème assurant l’existence et l’unicité des valeurs de Shapley
Le théorème de Shapley nous dit qu’il existe une unique répartition satisfaisant quatre propriétés, assurant que la répartition du gain entre les joueurs est équitable.
Soit ![]() la fonction caractéristique d’un jeu de
la fonction caractéristique d’un jeu de ![]() joueurs, telle que précédemment définie.
joueurs, telle que précédemment définie.
Soit ![]() telle que :
telle que : ![]()
Il existe une et une seul fonction ![]() vérifiant les contraintes suivantes :
vérifiant les contraintes suivantes :
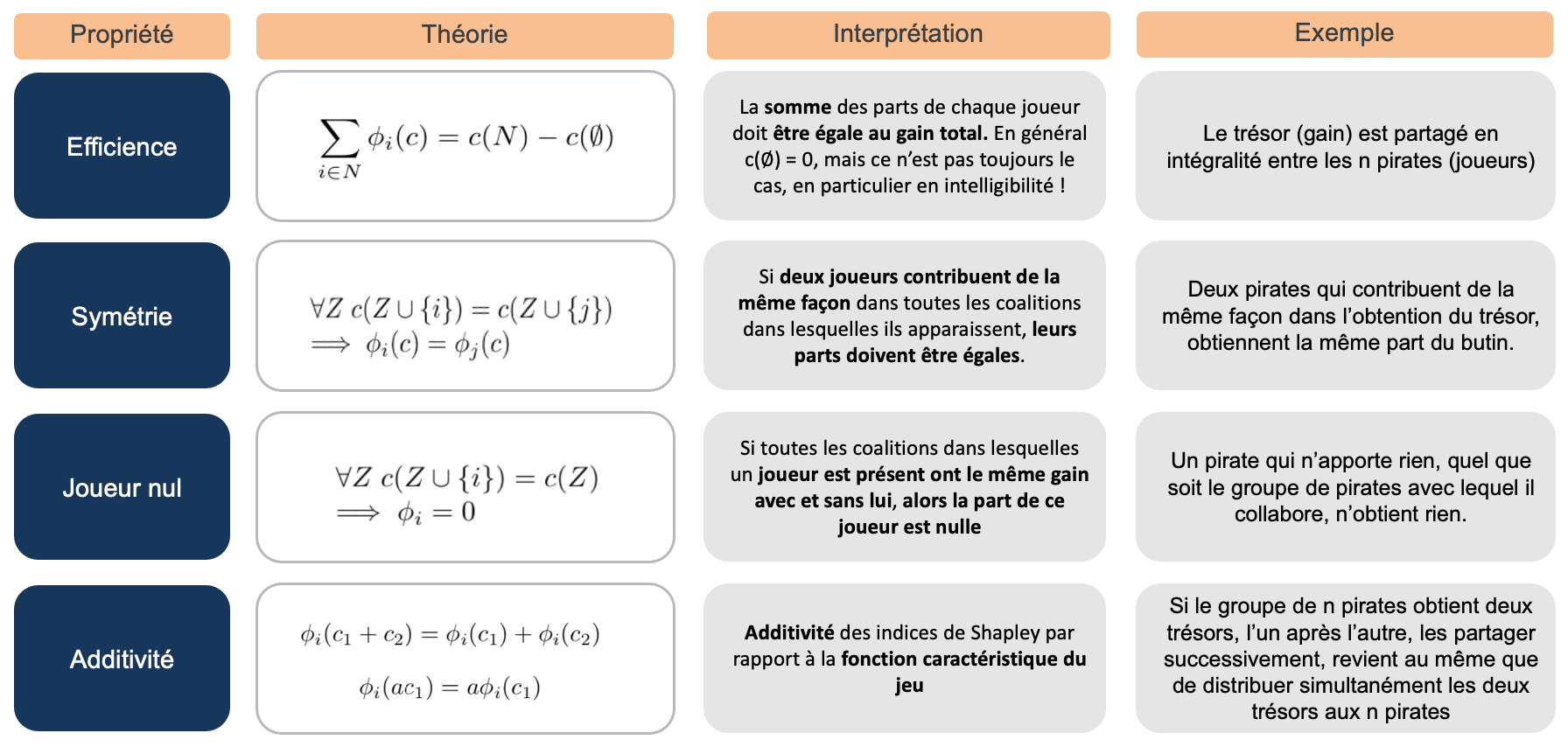
Figure 4. Synthèse et interprétation des propriétés vérifiées par les valeurs de Shapley
Cette fonction est définie par :
(2) ![Rendered by QuickLaTeX.com \begin{align*} \phi_{i}(c) &=\sum_{Z \subseteq N \backslash \{i\} }\frac{|Z| !(n-|Z|-1) !}{n !} \times[c(Z\cup \{i\})-c(Z)] \end{align*}](https://www.quantmetry.com/wp-content/ql-cache/quicklatex.com-4f0d859a19450d913573e8f2a8d131c8_l3.png)
On précise que ce résultat ne nécessite pas d’hypothèses particulières sur la fonction caractéristique ![]() .
.
Interprétation du calcul des valeurs de Shapley
Pour obtenir ![]() il faut donc calculer pour chaque coalition
il faut donc calculer pour chaque coalition ![]() dans laquelle le joueur
dans laquelle le joueur ![]() n’apparaît pas la différence de gain
n’apparaît pas la différence de gain ![]() . Cela permet de comparer le gain obtenu de la coalition avec et sans ce joueur, afin de mesurer son impact lorsqu’il collabore avec cet ensemble de joueurs.
. Cela permet de comparer le gain obtenu de la coalition avec et sans ce joueur, afin de mesurer son impact lorsqu’il collabore avec cet ensemble de joueurs.
Si cette différence est positive, cela signifie que le joueur i contribue positivement à cette coalition. A l’inverse, si la différence est négative, cela signifie que le joueur i pénalise le groupe. Enfin, si la différence est nulle, cela indique que le joueur i n’apporte rien à ce groupe.
On calcule ensuite la moyenne de ces écarts sur toutes les coalitions dans lesquelles le joueur i apparaît.
On peut réécrire de la manière suivante la formule, pour mieux comprendre le calcul du nombre de coalitions dans lesquelles le joueur i apparaît, on regroupe les coalitions par tailles :
(3) ![Rendered by QuickLaTeX.com \begin{align*} \phi_{i} &= \frac{1}{n}\sum_{k=0}^{n-1} {\dbinom{n-1}{k}}^{-1} \sum_{\substack{Z \subset N \backslash \{i\} \\ |Z| = k}} [c(Z\cup \{i\})-c(Z)] \end{align*}](https://www.quantmetry.com/wp-content/ql-cache/quicklatex.com-401a3fd0711c56e91f9e0a4cd79f0eb8_l3.png)
Cette réécriture de la formule ![]() montre bien que l’on fait la moyenne des différences.
montre bien que l’on fait la moyenne des différences.
Le dénombrement est le suivant : on classe les coalitions ![]() par cardinal ; on fait la moyenne des écarts pour toutes les coalitions
par cardinal ; on fait la moyenne des écarts pour toutes les coalitions ![]() de mêmes cardinaux. Pour une taille de coalition
de mêmes cardinaux. Pour une taille de coalition ![]() il y a
il y a ![]() coalitions possibles.
coalitions possibles.
On moyenne ensuite ces résultats intermédiaires : il y a n tailles de coalitions différentes, l’ensemble vide étant la coalition de cardinal 0.
L’intérêt principal de la répartition par les valeurs de Shapley, est la simplicité de son expression (n coefficients, sommables) tout en tenant compte des contributions du joueur i aux coalitions auxquelles il appartient. Autrement dit elle tient compte des interactions entre joueurs.
Faire le pont entre la théorie des jeux coopératifs et le Machine Learning

Figure 5. Pour passer de la théorie des jeux au machine learning, les joueurs deviennent les modalités des variables explicatives, le gain à répartir devient la différence entre prévision et moyenne des prévisions.
Pour passer de la théorie des jeux au Machine Learning, les joueurs deviennent les modalités des variables explicatives. Le gain à répartir devient la différence entre prévision et moyenne des prévisions.
En Machine Learning, on souhaite expliquer la prédiction ![]() associée à une observation
associée à une observation ![]() .
.
A chaque couple observation-prédiction ![]() , est associée un jeu :
, est associée un jeu :
- Les joueurs sont les valeurs
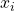 prises par
prises par 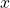 sur chaque variable d’entrée.
sur chaque variable d’entrée. - La quantité à répartir équitablement entre tous ces joueurs est la différence entre la prédiction
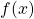 et la moyenne des prédictions
et la moyenne des prédictions ![Rendered by QuickLaTeX.com \mathbb{E}[f(X)]](https://www.quantmetry.com/wp-content/ql-cache/quicklatex.com-4eb065567ba9c70611a8b59c5a19d1f4_l3.png) .
. - La fonction caractéristique du jeu est :
![Rendered by QuickLaTeX.com c(u) = \mathbb{E}[f(X)|X_{u} = x_{u}]](https://www.quantmetry.com/wp-content/ql-cache/quicklatex.com-9f39d2dfd96175ebb9ede60c30f43d59_l3.png) , définie pour toute coalition
, définie pour toute coalition 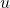 de valeurs
de valeurs 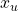 de
de 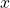 (voir [1]). Si
(voir [1]). Si 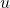 est la coalition
est la coalition 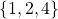 (première, deuxième et quatrième variables d’entrée), la notation
(première, deuxième et quatrième variables d’entrée), la notation 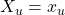 correspond à l’évènement
correspond à l’évènement 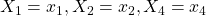 .
.
La valeur de Shapley associée à une modalité ![]() est donc définie par :
est donc définie par :
(4) ![Rendered by QuickLaTeX.com \begin{equation*} \phi_{i}(f,x)= \sum_{u \subseteq \{1,\ldots,n \} \backslash i} \frac{(n-|u|-1) !|u| !}{n !}\;[\mathbb{E}[f(X)|X_{u \cup\{i\}} = x_{u \cup\{i\}}] - \mathbb{E}[f(X)|X_{u} = x_{u}]] \end{equation*}](https://www.quantmetry.com/wp-content/ql-cache/quicklatex.com-f59054c585c8f071cadcf5ccefc153da_l3.png)
La somme des valeurs de Shapley d’une observation ![]() est égale à l’écart entre la prévision
est égale à l’écart entre la prévision ![]() et la moyenne des prévisions
et la moyenne des prévisions ![]() :
:
(5) ![Rendered by QuickLaTeX.com \begin{equation*} f(x)-\mathbb{E}[f(X)]=\sum_{i=1}^{p} \phi_{i} \end{equation*}](https://www.quantmetry.com/wp-content/ql-cache/quicklatex.com-50e49862ac932f5147bbaa4897bb7f00_l3.png)
On insiste sur le fait que ce n’est pas la prévision ![]() elle-même que l’on répartit entre les joueurs (valeurs)
elle-même que l’on répartit entre les joueurs (valeurs) ![]() , mais la quantité
, mais la quantité ![]() . Autrement dit, le coefficient
. Autrement dit, le coefficient ![]() explique comment les valeurs
explique comment les valeurs ![]() contribuent à décaler la prévision
contribuent à décaler la prévision ![]() de la moyenne
de la moyenne ![]() des prévisions.
des prévisions.
Deux modalités xi et xj prises isolément peuvent n’avoir aucun pouvoir de prédiction, alors qu’elles peuvent être très informatives une fois couplées ensemble. L’intérêt de l’approche basée sur le théorème de Shapley est de tenir compte des effets d’interactions, car la contribution de chaque valeur xi est moyennée dans chacune des coalitions de valeurs u auxquelles elle appartient.
De plus, les valeurs de Shapley en Machine Learning conservent toutes les propriétés des valeurs de Shapley en théorie des jeux coopératifs.
De la Théorie à la pratique …
Estimer numériquement les valeurs de Shapley avec SHAP
Si la définition mathématique des valeurs de Shapley en intelligibilité est relativement simple, leur estimation, elle, n’est pas aisée. Le calcul d’un coefficient de Shapley, en reprenant la formule (2) pose deux difficultés :
- Estimer les espérances conditionnelles ;
- Faire face à l’explosion combinatoire du nombre de coalitions à parcourir, lorsque le nombre n de joueurs augmente. Le nombre de coalitions à parcourir est exponentiel, en 2n.
La bibliothèque Python SHAP propose différents algorithmes d’estimation, agnostiques au modèle ou au contraire, spécifiques à un type de modèle.
En tout la bibliothèque contient cinq algorithmes. Nous ne rentrerons pas ici dans les détails de chaque algorithme.
- Kernel Explainer [3]: agnostique au modèle, fonctionne pour tout type de modèle.
- Tree Explainer [2]: pour les modèles basés sur les arbres de décision.
- Deep Explainer : pour les réseaux de neurones.
- Gradient Explainer : pour les réseaux de neurones.
- Linear Explainer : pour des modèles linéaires, souvent déjà intelligibles.
Des résultats difficiles à valider
En Machine Learning, après avoir été entraîné sur un jeu d’entraînement, la qualité d’un modèle prédictif est évaluée, a posteriori, sur un jeu de test grâce à des mesures d’erreurs.
En intelligibilité, il n’existe pas de mesure pour évaluer les résultats d’un algorithme d’intelligibilité. On pourrait imaginer utiliser une mesure de précision, mais cela supposerait de disposer a priori, de résultats d’intelligibilité validés, par les métiers par exemple. Or si les experts/opérateurs métiers sont capables d’expliquer eux-mêmes les prédictions du modèle, cela signifie que le modèle est déjà intelligible. L’intelligibilité n’a alors pas lieu d’être.
On voit donc que si l’on doit utiliser un algorithme d’intelligibilité pour expliquer les sorties d’un algorithme prédictif, c’est qu’il n’est pas possible de les expliquer autrement. Si un expert métier peut valider ou invalider certaines prédictions fournies par l’algorithme de Machine Learning, il demeure impossible de quantifier la précision et la justesse de l’algorithme d’intelligibilité a posteriori.
Si les experts métiers peuvent permettre de détecter des explications aberrantes dans les résultats d’intelligibilité, le Data Scientist doit s’assurer de son côté que les modèles d’intelligibilité qu’il utilise sont bien définis, et connaître leurs hypothèses, leurs limites.
Une mauvaise utilisation d’un algorithme d’intelligibilité fait courir le risque de se retrouver avec deux modèles mal compris : le modèle prédictif boîte noire et le modèle d’intelligibilité lui-même, et ce, alors même que l’on souhaitait augmenter l’intelligibilité du premier modèle.
Il est donc tout aussi important de comprendre les modèles d’intelligibilité que les modèles de Machine Learning.
Conclusion
Les valeurs de Shapley appliquées au Machine Learning sont une technique d’intelligibilité locale, expliquant la prédiction associée à une observation. Elles permettent, pour une observation donnée, de quantifier l’impact de chaque feature de cette observation sur la prédiction qui lui est associée par le modèle.
L’avantage des valeurs de Shapley est qu’il n’y a pas d’hypothèses particulières à satisfaire et qu’elles prennent en compte les interactions entre valeurs d’entrée (feature) pour déterminer leur rôle dans la prédiction du modèle.
Pour ce qui est de leur estimation en Python, la bibliothèque SHAP est la bibliothèque de référence. Elle fournit différents algorithmes d’estimation en fonction du type de modèle prédictif utilisé, ainsi que de nombreuses visualisations.
Une difficulté subsiste malgré tout en intelligibilité, et non des moindres : l’absence, en général, de valeurs cibles pour valider les résultats. Il est donc d’autant plus important de bien comprendre les limites des valeurs de Shapley, tant théoriques (définition mathématique) que pratiques (estimation) avant de les utiliser.
Références
[1] S. Lundberg and S.-L. Lee. A unified appoach to interpreting model predictions. 2017
[2] L. S. Shapley. A value for n-person games.Contributions to the Theory of Games, pages 307–317,1953.
[3] S.-I. Lee S. Lundberg, G. Erion. Consistent individualized feature attribution for tree ensembles. 2018

